دائرة على المستوى الإحداثي. الدرس اللامنهجي - دائرة الأرقام

يتم تخصيص الكثير من الوقت لدائرة الأرقام في الصف العاشر. ويرجع ذلك إلى أهمية هذا الكائن الرياضي لمقرر الرياضيات بأكمله.

قيمة عظيمة ل امتصاص جيدالمواد لديها الاختيار الصحيح للوسائل التعليمية. وتشمل هذه الأدوات الأكثر فعالية دروس الفيديو. في مؤخرايصلون إلى ذروة الشعبية. لذلك، لم يتخلف المؤلف عن الزمن وقام بتطوير مثل هذا الدليل الرائع لمساعدة معلمي الرياضيات - درس فيديو حول موضوع "دائرة الأرقام على المستوى الإحداثي".

يستمر هذا الدرس 15:22 دقيقة. انها عمليا الحد الأقصى للوقتوالتي يمكن للمدرس أن ينفق عليها بشكل مستقل في شرح المادة المتعلقة بالموضوع. نظرا لأن شرح المواد الجديدة يستغرق الكثير من الوقت، فمن الضروري اختيار المهام والتمارين الأكثر فعالية للتوحيد، وكذلك تحديد درس آخر حيث سيقوم الطلاب بحل المهام حول هذا الموضوع.

يبدأ الدرس بصورة دائرة رقمية في نظام الإحداثيات. يبني المؤلف هذه الدائرة ويشرح أفعاله. ثم يقوم المؤلف بتسمية نقاط تقاطع دائرة الأعداد مع محاور الإحداثيات. يوضح ما يلي إحداثيات نقاط الدائرة في الأرباع المختلفة.

بعد ذلك يذكرنا المؤلف كيف تبدو معادلة الدائرة. ويعرض على المستمعين نموذجين يصوران بعض النقاط على الدائرة. بفضل هذا، يوضح المؤلف في الخطوة التالية كيفية العثور على إحداثيات النقاط الموجودة على الدائرة المقابلة لأرقام معينة محددة في القوالب. ينتج عن ذلك جدول قيم للمتغيرين x و y في معادلة الدائرة.

بعد ذلك، نقترح النظر في مثال حيث يكون من الضروري تحديد إحداثيات النقاط على الدائرة. وقبل البدء في حل المثال تم تقديم بعض الملاحظات التي تساعد في حله. ومن ثم يظهر على الشاشة حل كامل ومنظم بشكل واضح ومصور. توجد أيضًا جداول هنا تسهل فهم جوهر المثال.

ثم يتم النظر في ستة أمثلة أخرى، وهي أقل استهلاكا للوقت من الأول، ولكنها لا تقل أهمية وتعكس الفكرة الرئيسية للدرس. هنا يتم عرض الحلول كاملة، مع قصة مفصلة وعناصر الوضوح. أي أن الحل يحتوي على رسومات توضح تقدم الحل، وتدوينًا رياضيًا يشكل الثقافة الرياضية لدى الطلاب.

قد يقتصر المعلم على الأمثلة التي تمت مناقشتها في الدرس، ولكن هذا قد لا يكون كافيا لتعلم المواد عالية الجودة. لذلك، فإن اختيار المهام التي يجب تعزيزها أمر في غاية الأهمية.

يمكن أن يكون الدرس مفيدا ليس فقط للمعلمين، الذين يكون وقتهم محدودا باستمرار، ولكن أيضا للطلاب. خاصة بالنسبة لأولئك الذين يتلقون التعليم الأسري أو يشاركون في التعليم الذاتي. يمكن استخدام المواد من قبل الطلاب الذين فاتتهم درس حول هذا الموضوع.

فك تشفير النص:

موضوع درسنا هو "الدائرة الرقمية على المستوى الإحداثي"

نحن بالفعل على دراية بنظام الإحداثيات المستطيل الديكارتي xOy (x o y). في نظام الإحداثيات هذا سوف نضع دائرة الرقمبحيث يكون مركز الدائرة محاذياً لأصل الإحداثيات، ويُؤخذ نصف قطرها كقطعة مقياس.

يتم دمج نقطة البداية A لدائرة الأرقام مع نقطة ذات إحداثيات (1;0)، وB - مع نقطة (0;1)، وC - مع (-1;0) (ناقص واحد، صفر)، وD - مع (0؛ - 1)(صفر، ناقص واحد).

(انظر الشكل 1)

نظرًا لأن كل نقطة في دائرة الأرقام لها إحداثياتها الخاصة في نظام xOy (x o y)، فبالنسبة لنقاط الربع الأول yx أكبر من الصفر وy أكبر من الصفر؛

ICH الربع الثاني أقل من الصفرواللعبة أكبر من الصفر،

لنقاط الربع الثالث ikx أقل من الصفر وyk أقل من الصفر،

وفي الربع الرابع ikx أكبر من الصفر وyk أقل من الصفر

بالنسبة لأي نقطة E (x;y) (مع الإحداثيات x, y) من دائرة الأرقام، فإن المتباينات -1≥ x≥ 1، -1≤y≥1 (x أكبر من أو يساوي سالب واحد، ولكن أقل من أو يساوي واحدًا؛ y أكبر من أو يساوي سالب واحد، ولكن أقل من أو يساوي واحدًا).

تذكر أن معادلة دائرة نصف قطرها R ومركزها عند نقطة الأصل لها الصيغة x 2 + y 2 = R 2 (مربع x زائد مربع y يساوي مربع er). وبالنسبة لدائرة الوحدة R = 1، فنحصل على x 2 + y 2 = 1

(مربع x زائد مربع y يساوي واحدًا).

دعونا نجد إحداثيات النقاط على دائرة الأرقام، والتي يتم عرضها في مخططين (انظر الشكل 2، 3)

دع النقطة E، التي تقابل

(باي بأربعة) - منتصف الربع الأول الموضح في الشكل. من النقطة E نخفض الخط المتعامد EK إلى الخط المستقيم OA وننظر إلى المثلث OEK. الزاوية AOE = 45 0، بما أن القوس AE يساوي نصف القوس AB. ولذلك، فإن المثلث OEK هو مثلث قائم الزاوية متساوي الساقين، حيث OK = EC. وهذا يعني أن الإحداثي والإحداثي للنقطة E متساويان، أي. × يساوي اللعبة. لإيجاد إحداثيات النقطة E نحل نظام المعادلات: (x تساوي y - المعادلة الأولى للنظام وx مربع زائد y مربع يساوي واحد - المعادلة الثانية للنظام). معادلة النظام، بدلاً من x، نعوض بـ y، نحصل على 2y 2 = 1 (اثنان y Square يساوي واحدًا)، حيث y = = (y يساوي واحدًا مقسومًا على جذر اثنين يساوي جذر اثنين مقسومًا على اثنين) (الإحداثي موجب)، وهذا يعني أن النقطة E في نظام الإحداثيات المستطيل لها إحداثيات (،)(جذر اثنين مقسومًا على اثنين، جذر اثنين مقسومًا على اثنين).

بالتفكير بطريقة مماثلة، نجد إحداثيات النقاط المقابلة للأرقام الأخرى للتخطيط الأول ونحصل على: النقطة المقابلة لها إحداثيات (-،) (ناقص جذر اثنين مقسومًا على اثنين، جذر اثنين مقسومًا على اثنين) ; لـ - (- ,-) (ناقص جذر اثنين مقسومًا على اثنين، ناقص جذر اثنين مقسومًا على اثنين)؛ لـ (سبعة باي على أربعة) (،)(جذر اثنين مقسومًا على اثنين، ناقص جذر اثنين مقسومًا على اثنين).

دع النقطة D تتوافق مع (الشكل 5). دعونا نسقط العمودي من DP(de pe) إلى OA وننظر إلى المثلث ODP. وتر هذا المثلث OD يساوي نصف قطر دائرة الوحدة، أي واحد، والزاوية DOP تساوي ثلاثين درجة، لأن القوس AD = digi AB (a de يساوي ثلث a be)، و القوس AB يساوي تسعين درجة. لذلك، DP = (de pe يساوي نصف O de يساوي نصفًا) بما أن الساق الواقعة مقابل الزاوية الثلاثين درجة تساوي نصف الوتر، أي أن y = (y يساوي نصفًا) . بتطبيق نظرية فيثاغورس، نحصل على OR 2 = OD 2 - DP 2 (o pe² يساوي o de² ناقص de pe²)، لكن OR = x (o pe يساوي x). وهذا يعني x 2 = OD 2 - DP 2 =

هذا يعني أن x 2 = (مربع x يساوي ثلاثة أرباع) وx = (x يساوي جذر ثلاثة في اثنين).

X موجب، لأن هو في الربع الأول. لقد وجدنا أن النقطة D في نظام إحداثي مستطيل لها إحداثيات (،) جذر ثلاثة مقسومًا على اثنين، نصف.

بالتفكير بطريقة مماثلة، سنجد إحداثيات النقاط المقابلة للأرقام الأخرى للتخطيط الثاني ونكتب جميع البيانات التي تم الحصول عليها في الجداول:

دعونا نلقي نظرة على الأمثلة.

مثال 1. أوجد إحداثيات النقاط على دائرة الأرقام: أ) C 1 ()؛

ب) ج 2 ()؛ ج) ج 3 (41π)؛ د) ج 4 (- 26π). (Tse واحد يقابل خمسة وثلاثين pi في أربعة، وtse اثنان يقابل ناقص تسعة وأربعين pi في ثلاثة، وtse ثلاثة يقابل واحد وأربعين pi، وtse أربعة يقابل ناقص ستة وعشرين pi).

حل. دعونا نستخدم العبارة التي تم الحصول عليها سابقًا: إذا كانت النقطة D من دائرة الأرقام تتوافق مع الرقم t، فإنها تتوافق مع أي رقم من النموذج t + 2πk(te زائد ذروتين)، حيث ka هو أي عدد صحيح، أي. kϵZ (كا ينتمي إلى z).

أ) نحصل على = ∙ π = (8 +) ∙π = + 2π ∙ 4. (خمسة وثلاثون باي في أربعة يساوي خمسة وثلاثين في أربعة، مضروبًا في باي يساوي مجموع ثمانية وثلاثة أرباع، مضروبًا في باي يساوي ثلاثة باي في أربعة زائد حاصل ضرب اثنين باي في أربعة). وهذا يعني أن الرقم خمسة وثلاثين باي في أربعة يتوافق مع نفس النقطة على دائرة الأعداد مثل الرقم ثلاثة باي في أربعة. باستخدام الجدول 1، نحصل على C 1 () = C 1 (- ;) .

ب) شبيهة بالإحداثيات C 2: = ∙ π = - (16 + ∙π = + 2π ∙ (- 8) وهذا يعني أن الرقم

يتوافق مع نفس النقطة على دائرة الأرقام مثل الرقم. والرقم يتوافق مع نفس النقطة الموجودة على دائرة الأعداد مثل الرقم

(أظهر التصميم الثاني والجدول 2). بالنسبة لنقطة ما لدينا x = , y =.

ج) 41π = 40π + π = π + 2π ∙ 20. وهذا يعني أن الرقم 41π يتوافق مع نفس النقطة على دائرة الأرقام مثل الرقم π - هذه نقطة ذات إحداثيات (-1؛ 0).

د) - 26π = 0 + 2π ∙ (- 13)، أي أن الرقم - 26π يتوافق مع نفس النقطة على دائرة الأعداد مثل الرقم صفر - هذه نقطة بإحداثيات (1;0).

مثال 2. ابحث عن النقاط الموجودة على دائرة الأرقام ذات الإحداثيات y =

حل. الخط المستقيم y = يقطع دائرة الأعداد بنقطتين. النقطة الأولى تمثل رقمًا، والنقطة الثانية تمثل رقمًا،

لذلك، نحصل على جميع النقاط عن طريق إضافة دورة كاملة 2πk حيث يوضح k عدد الدورات الكاملة التي تقوم بها النقطة، أي. نحن نحصل،

ولأي رقم جميع الأرقام من النموذج + 2πk. في كثير من الأحيان في مثل هذه الحالات يقولون أنهم تلقوا سلسلتين من القيم: + 2πk، + 2πk.

مثال 3. ابحث عن النقاط على دائرة الأرقام التي تحتوي على الإحداثي السيني x = واكتب الأرقام التي تتوافق معها.

حل. مستقيم X= يتقاطع مع دائرة الأعداد في نقطتين. نقطة واحدة تقابل رقمًا (انظر التخطيط الثاني)،

وبالتالي أي رقم على الصورة + 2πk. والنقطة الثانية تقابل رقمًا، وبالتالي أي رقم على الصورة + 2πk. يمكن تغطية هاتين السلسلتين من القيم في إدخال واحد: ± + 2πk (زائد ناقص اثنين pi بمقدار ثلاثة زائد اثنين pi).

مثال 4. ابحث عن النقاط ذات الإحداثيات على دائرة الأعداد في> واكتب الأرقام التي تتوافق معها.

الخط المستقيم y = يتقاطع مع دائرة الأعداد عند نقطتين M و P. والمتباينة y > تقابل نقاط القوس المفتوح MR، وهذا يعني أقواس بلا نهايات (أي بدون u)، عند التحرك حول الدائرة عكس اتجاه عقارب الساعة ، بدءًا من النقطة M وينتهي عند النقطة P. وهذا يعني أن جوهر التدوين التحليلي للقوس MR هو عدم المساواة< t < (тэ больше, чем пи на три, но меньше двух пи на три) , а сама аналитическая запись дуги имеет вид + 2πk < t < + 2πk(тэ больше, чем пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).

مثال5. ابحث عن النقاط الإحداثية على دائرة الأعداد في < и записать, каким числам t они соответствуют.

الخط المستقيم y = يقطع دائرة الأعداد عند نقطتين M و P. والمتباينة y< соответствуют точки открытой дуги РМ при движении по окружности против часовой стрелки, начиная с точки Р, а заканчивая в точке М. Значит, ядром аналитической записи дуги РМ является неравенство < t < (тэ больше, чем минус четыре пи на три, но меньше пи на три) , а сама аналитическая запись дуги имеет вид

2πك< t < + 2πk (тэ больше, чем минус четыре пи на три плюс два пи ка, но меньше пи на три плюс два пи ка).

مثال 6. ابحث عن النقاط ذات الإحداثي الإحداثي على دائرة الأعداد X> واكتب الأرقام التي تتوافق معها.

الخط المستقيم x = يتقاطع مع دائرة الأعداد عند نقطتين M و P. المتباينة x > تتوافق مع نقاط القوس المفتوح PM عند التحرك على طول الدائرة عكس اتجاه عقارب الساعة مع البداية عند النقطة P التي تقابلها، والنهاية عند النقطة م، وهو ما يتوافق. وهذا يعني أن جوهر التدوين التحليلي لقوس PM هو عدم المساواة< t <

(te أكبر من ناقص اثنين باي في ثلاثة، ولكن أقل من اثنين باي في ثلاثة)، والترميز التحليلي للقوس نفسه له الشكل + 2πk< t < + 2πk (тэ больше, чем минус два пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).

مثال 7. ابحث عن النقاط ذات الإحداثي الإحداثي على دائرة الأعداد X < и записать, каким числам t они соответствуют.

الخط المستقيم x = يقطع دائرة الأعداد عند نقطتين M و P. المتباينة x< соответствуют точки открытой дуги МР при движении по окружности против часовой стрелки с началом в точке М, которая соответствует, и концом в точке Р, которая соответствует. Значит, ядром аналитической записи дуги МР является неравенство < t <

(te أكبر من اثنين pi في ثلاثة، ولكن أقل من أربعة pi في ثلاثة)، والترميز التحليلي للقوس نفسه له الشكل + 2πk< t < + 2πk (тэ больше, чем два пи на три плюс два пи ка, но меньше четырех пи на три плюс два пи ка).

دائرة الأرقامهي دائرة الوحدة التي تتوافق نقاطها مع أرقام حقيقية معينة.

دائرة الوحدة هي دائرة نصف قطرها 1.

منظر عام لدائرة الأعداد.

1) يؤخذ نصف القطر كوحدة قياس.

2) يقسم القطران الأفقي والرأسي دائرة الأعداد إلى أربعة أرباع (انظر الشكل). ويطلق عليهم على التوالي الربع الأول والثاني والثالث والرابع.

3) يُشار إلى القطر الأفقي بالرمز AC، وتكون النقطة A أقصى اليمين.
يُشار إلى القطر العمودي بـ BD، حيث تكون النقطة B هي أعلى نقطة.
على التوالى:

الربع الأول هو القوس AB

الربع الثاني – قوس قبل الميلاد

الربع الثالث - قرص مضغوط القوس

الربع الرابع - قوس DA

4) نقطة بداية دائرة الأعداد هي النقطة أ.

يمكن إجراء العد على طول دائرة الأرقام إما في اتجاه عقارب الساعة أو عكس اتجاه عقارب الساعة.
يسمى العد من النقطة A عكس اتجاه عقارب الساعة اتجاه إيجابي.
يسمى العد من النقطة A في اتجاه عقارب الساعة الاتجاه السلبي.

دائرة الأعداد على المستوى الإحداثي

يتوافق مركز نصف قطر دائرة الأرقام مع الأصل (رقم 0).

القطر الأفقي يتوافق مع المحور س، عمودي – محاور ذ.

نقطة البداية A لدائرة الأعداد تقع على المحور سولها إحداثيات (1؛ 0).

قيمسوذفي أرباع دائرة الأرقام:

القيم الأساسية لدائرة الأرقام:

أسماء ومواقع النقاط الرئيسية على دائرة الأعداد:

كيف تتذكر أسماء دوائر الأرقام

هناك العديد من الأنماط البسيطة التي ستساعدك على تذكر الأسماء الأساسية لدائرة الأرقام بسهولة.

قبل أن نبدأ، دعونا نذكرك: يتم العد في الاتجاه الإيجابي، أي من النقطة A (2π) عكس اتجاه عقارب الساعة.

1) لنبدأ بالنقاط القصوى على محاور الإحداثيات.

نقطة البداية هي 2π (أقصى اليمين على المحور X، يساوي 1).

كما تعلم، 2π هو محيط الدائرة. هذا يعني أن نصف الدائرة هو 1π أو π. محور Xيقسم الدائرة إلى النصف بالضبط. وبناء على ذلك، أقصى نقطة على اليسار على المحور Xيساوي -1 يسمى π.

أعلى نقطة على المحور في، يساوي 1، يقسم نصف الدائرة العلوي إلى نصفين. هذا يعني أنه إذا كان نصف الدائرة هو π، فإن نصف نصف الدائرة هو π/2.

وفي الوقت نفسه، π/2 هو أيضًا ربع الدائرة. لنعد ثلاثة أرباع من الأول إلى الثالث - وسنصل إلى أدنى نقطة على المحور في، يساوي -1. أما إذا كان يشتمل على ثلاثة أرباع، فإن اسمه 3ط/2.

2) الآن دعنا ننتقل إلى النقاط المتبقية. يرجى ملاحظة: جميع النقاط المتقابلة لها نفس البسط - وهذه نقاط متقابلة بالنسبة للمحور في، سواء بالنسبة إلى مركز المحاور، أو بالنسبة إلى المحور X. سيساعدنا هذا في معرفة قيم نقاطهم دون حشو.

ما عليك سوى أن تتذكر معنى نقاط الربع الأول: π/6، π/4 وπ/3. وبعد ذلك سوف "نرى" بعض الأنماط:

- نسبة إلى المحور yعند نقاط الربع الثاني، مقابل نقاط الربع الأول، تكون الأرقام في البسط أقل بمقدار 1 من حجم المقامات. على سبيل المثال، خذ النقطة π/6. النقطة المقابلة لها بالنسبة للمحور فيلديه أيضًا 6 في المقام و5 في البسط (1 أقل). أي أن اسم هذه النقطة هو: 5π/6. النقطة المقابلة لـ π/4 لها أيضًا 4 في المقام و3 في البسط (1 أقل من 4) - أي أنها نقطة 3π/4.
النقطة المقابلة لـ π/3 لها أيضًا 3 في المقام، و1 أقل في البسط: 2π/3.

- نسبة إلى مركز محاور الإحداثياتكل شيء على العكس من ذلك: الأرقام الموجودة في بسط النقاط المتقابلة (في الربع الثالث) أكبر بمقدار 1 من قيمة المقامات. لنأخذ النقطة π/6 مرة أخرى. النقطة المقابلة لها بالنسبة للمركز لديها أيضًا 6 في المقام، وفي البسط يكون الرقم أكبر بمقدار 1 - أي 7π/6.

النقطة المقابلة للنقطة π/4 لها أيضًا 4 في المقام، وفي البسط يكون الرقم 1 إضافي: 5π/4.
النقطة المقابلة للنقطة π/3 لها أيضًا 3 في المقام، وفي البسط يكون الرقم 1 إضافي: 4π/3.

- نسبة إلى المحور X(الربع الرابع)الأمر أكثر تعقيدًا. هنا تحتاج إلى إضافة رقم أقل بمقدار 1 إلى قيمة المقام - سيكون هذا المجموع مساوياً للجزء الرقمي من بسط النقطة المقابلة. لنبدأ مرة أخرى مع π/6. لنضيف إلى قيمة المقام التي تساوي 6 رقمًا أقل من هذا الرقم بمقدار 1 - أي 5. نحصل على: 6 + 5 = 11. وهذا يعني أنه مقابل للمحور Xسيكون للنقطة 6 في المقام و11 في البسط - أي 11π/6.

النقطة π/4. نضيف إلى قيمة المقام رقما أقل 1: 4 + 3 = 7. وهذا يعني أنه مقابل للمحور Xتحتوي النقطة على 4 في المقام و7 في البسط - أي 7π/4.
النقطة π/3. المقام هو 3. نضيف إلى 3 رقمًا أصغر بمقدار واحد - أي 2. نحصل على 5. هذا يعني أن النقطة المقابلة لها بها 5 في البسط - وهذه هي النقطة 5π/3.

3) نمط آخر لنقاط منتصف الأرباع. من الواضح أن مقامهم هو 4. دعونا ننتبه إلى البسطين. بسط منتصف الربع الأول هو 1π (لكن ليس من المعتاد كتابة 1). بسط منتصف الربع الثاني هو 3π. بسط منتصف الربع الثالث هو 5π. بسط منتصف الربع الرابع هو 7π. اتضح أن بسط الأرباع الوسطى تحتوي على الأعداد الأربعة الفردية الأولى بترتيب تصاعدي:
(1)ط، 3ط، 5ط، 7ط.
وهذا أيضًا بسيط جدًا. نظرًا لأن نقاط المنتصف لجميع الأرباع تحتوي على 4 في المقام، فإننا نعرف بالفعل أسمائها الكاملة: π/4، 3π/4، 5π/4، 7π/4.

مميزات دائرة الأعداد. المقارنة مع خط الأعداد.

كما تعلمون، على خط الأعداد، كل نقطة تقابل رقمًا واحدًا. على سبيل المثال، إذا كانت النقطة A على الخط تساوي 3، فلا يمكن أن تساوي أي رقم آخر.

الأمر مختلف على دائرة الأعداد لأنها دائرة. على سبيل المثال، من أجل الانتقال من النقطة A من الدائرة إلى النقطة M، يمكنك القيام بذلك كما لو كنت على خط مستقيم (تمرير قوس فقط)، أو يمكنك الالتفاف حول دائرة كاملة، ثم الوصول إلى النقطة M. خاتمة:

دع النقطة M تساوي عددا ما. كما نعلم، محيط الدائرة هو 2π. هذا يعني أنه يمكننا كتابة نقطة على الدائرة t بطريقتين: t أو t + 2π. هذه قيم متكافئة.
أي أن t = t + 2π. الفرق الوحيد هو أنك في الحالة الأولى وصلت إلى النقطة M فورًا دون عمل دائرة، وفي الحالة الثانية قمت بعمل دائرة، ولكن انتهى بك الأمر عند نفس النقطة M. يمكنك عمل مئتين أو ثلاث أو مائتين من هذا القبيل دوائر. إذا قمنا بالإشارة إلى عدد الدوائر بالحرف ك، ثم نحصل على تعبير جديد:
ر = ر + 2π ك.

ومن هنا الصيغة:

معادلة الدائرة العددية
(المعادلة الثانية موجودة في قسم "جيب التمام، وجيب التمام، والظل، وظل التمام"):

س 2 + ص 2 = 1

نقدم انتباهكم إلى درس فيديو حول موضوع "دائرة الأرقام". يتم إعطاء تعريف لما هي الجيب وجيب التمام والظل وظل التمام والوظائف ذ= خطيئة س, ذ= كوس س, ذ= tg س, ذ= ctg سلأي وسيطة رقمية. نحن نعتبر المسائل القياسية للمراسلات بين الأرقام والنقاط في دائرة أرقام الوحدة للعثور على نقطة واحدة لكل رقم، وعلى العكس من ذلك، للعثور على مجموعة من الأرقام المقابلة لكل نقطة.

الموضوع: عناصر نظرية الدوال المثلثية

الدرس: دائرة الأعداد

هدفنا المباشر هو تحديد الدوال المثلثية: التجويف, جيب التمام, الظل, ظل التمام-

يمكن رسم الوسيطة الرقمية على خط إحداثي أو على دائرة.

وتسمى هذه الدائرة دائرة عددية أو دائرة الوحدة، لأن للراحة، خذ دائرة مع

على سبيل المثال، إذا أعطيت نقطة، ضع علامة عليها على خط الإحداثيات

و على دائرة الرقم.

عند العمل مع دائرة الأعداد، تم الاتفاق على أن الحركة عكس اتجاه عقارب الساعة هي اتجاه إيجابي، واتجاه عقارب الساعة هو اتجاه سلبي.

المهام النموذجية - تحتاج إلى تحديد إحداثيات نقطة معينة أو، على العكس من ذلك، العثور على نقطة من خلال إحداثياتها.

ينشئ خط الإحداثيات مراسلات فردية بين النقاط والأرقام. على سبيل المثال، الرقم يتوافق مع النقطة A بالإحداثيات

تتميز كل نقطة B ذات إحداثيات برقم واحد فقط - المسافة من 0 إلى المأخوذة بعلامة زائد أو ناقص.

في دائرة الأعداد، تعمل المراسلات الفردية في اتجاه واحد فقط.

على سبيل المثال، هناك نقطة B على الدائرة الإحداثية (الشكل 2)، طول القوس هو 1، أي. هذه النقطة تتوافق مع 1.

بالنظر إلى الدائرة، فإن طول الدائرة إذا كان هو طول دائرة الوحدة.

إذا أضفنا، نحصل على نفس النقطة B، ثم نصل أيضًا إلى النقطة B، ونطرح - أيضًا النقطة B.

خذ بعين الاعتبار النقطة ب: طول القوس = 1، ثم تميز الأرقام النقطة ب على دائرة الأعداد.

وبالتالي، فإن الرقم 1 يتوافق مع نقطة واحدة على دائرة الأرقام - النقطة B، والنقطة B تتوافق مع عدد لا نهائي من نقاط النموذج .

ينطبق ما يلي على دائرة الأعداد:

إذا كان ت. مإذا كانت دائرة الأرقام تتوافق مع رقم، فإنها تتوافق أيضًا مع رقم النموذج

يمكنك إجراء أي عدد تريده من الدورات الكاملة حول دائرة الأعداد في اتجاه إيجابي أو سلبي - النقطة هي نفسها. لذلك فإن المعادلات المثلثية لها عدد لا نهائي من الحلول.

على سبيل المثال، بالنظر إلى النقطة د. ما هي الأرقام التي تقابلها؟

نقيس القوس.

مجموعة جميع الأرقام المقابلة للنقطة D.

دعونا نلقي نظرة على النقاط الرئيسية في دائرة الأعداد.

طول المحيط بأكمله.

أولئك. يمكن أن يكون تسجيل إحداثيات متعددة مختلفًا .

دعونا نلقي نظرة على المسائل النموذجية في دائرة الأعداد.

1. المعطى : . البحث: نقطة على دائرة الأعداد.

دعنا نختار الجزء بأكمله:

من الضروري العثور على النقطة على دائرة الأرقام. ، ثم .

تتضمن هذه المجموعة أيضًا النقطة.

2. المعطى : . البحث: نقطة على دائرة الأعداد.

فمن الضروري العثور على ر.

ينتمي t.أيضًا إلى هذه المجموعة.

ومن خلال حل المسائل القياسية للمراسلات بين الأرقام والنقاط على دائرة الأعداد، اكتشفنا أنه لكل رقم يمكننا أن نجد نقطة واحدة، ولكل نقطة يمكننا أن نجد مجموعة من الأرقام التي تتميز بنقطة معينة.

قسّم القوس إلى ثلاثة أجزاء متساوية وحدد النقطتين M وN.

دعونا نجد جميع إحداثيات هذه النقاط.

إذن، هدفنا هو تحديد الدوال المثلثية. للقيام بذلك، علينا أن نتعلم كيفية تحديد وسيطة الدالة. لقد نظرنا إلى نقاط دائرة الوحدة وحللنا مشكلتين نموذجيتين - العثور على نقطة على دائرة الأعداد وكتابة جميع إحداثيات النقطة على دائرة الوحدة.

1. موردكوفيتش أ.ج. وغيرها الجبر الصف التاسع: كتاب مدرسي. للتعليم العام المؤسسات.- الطبعة الرابعة. - م: منيموسين، 2002.-192 ص: مريض.

2. موردكوفيتش أ.ج. وغيرها الجبر الصف التاسع: كتاب المشكلات لطلاب مؤسسات التعليم العام / A. G. Mordkovich، T. N. Mishustina، إلخ - الطبعة الرابعة. - م: منيموسين، 2002.-143 ص: مريض.

3. ماكاريشيف يو ن.الجبر. الصف التاسع: تعليمي لطلاب التعليم العام. المؤسسات / Yu.N. Makarychev، N. G. Mindyuk، K. I. Neshkov، I. E. Feoktistov. - الطبعة السابعة، مراجعة. وإضافية - م: منيموسين، 2008.

4. عليموف ش.أ.، كولياجين يو.إم.، سيدوروف يو.في. الجبر. الصف التاسع. الطبعة السادسة عشرة. - م.، 2011. - 287 ص.

5. موردكوفيتش إيه جي الجبر. الصف التاسع. في ساعتين الجزء 1. كتاب مدرسي لطلاب مؤسسات التعليم العام / A. G. Mordkovich، P. V. Semenov. – الطبعة الثانية عشر، محذوفة. - م: 2010. - 224 ص: مريض.

6. الجبر. الصف التاسع. في جزأين الجزء 2. كتاب المشكلات لطلاب مؤسسات التعليم العام / A. G. Mordkovich، L. A. Aleksandrova، T. N. Mishustina وآخرون؛ إد. ايه جي موردكوفيتش. - الطبعة الثانية عشرة، مراجعة. - م: 2010.-223 ص: مريض.

موردكوفيتش أ.ج. وغيرها الجبر الصف التاسع: كتاب المشكلات لطلاب مؤسسات التعليم العام / A. G. Mordkovich، T. N. Mishustina، إلخ - الطبعة الرابعة. - م: منيموسين، 2002.-143 ص: مريض.

№№ 531; 536; 537; 541; 552.

معادلة الدائرة على المستوى الإحداثي

التعريف 1. محور العدد ( خط الأعداد، خط الإحداثيات) الثور هو الخط المستقيم الذي تم تحديد النقطة O عليه الأصل (أصل الإحداثيات)(الشكل 1)، الاتجاه

يا → س

عبارة عن اتجاه إيجابيويتم وضع علامة على الجزء الذي يؤخذ طوله وحدة الطول.

التعريف 2. يُطلق على القطعة التي يتم أخذ طولها كوحدة للطول اسم المقياس.

كل نقطة على محور الأعداد لها إحداثيات تمثل عددًا حقيقيًا. إحداثيات النقطة O هي صفر. إحداثيات النقطة الاختيارية A الواقعة على الشعاع Ox تساوي طول المقطع OA. إحداثيات النقطة التعسفية A للمحور العددي التي لا تقع على شعاع Ox تكون سالبة، وفي القيمة المطلقة تساوي طول المقطع OA.

التعريف 3. نظام الإحداثيات الديكارتية المستطيلة أوكسي على المستوىاستدعاء اثنين بشكل متبادل عموديالمحاور العددية الثور وأوي مع نفس المقياسو نقطة مرجعية مشتركةعند النقطة O، بحيث يتم الدوران من الشعاع Ox بزاوية 90 درجة إلى الشعاع Oy في الاتجاه عكس عقارب الساعه(الصورة 2).

ملحوظة. يسمى نظام الإحداثيات الديكارتية المستطيلة أوكسي، كما هو موضح في الشكل 2 نظام الإحداثيات الصحيحعلى عكس أنظمة الإحداثيات اليسرى، حيث يتم تنفيذ دوران شعاع Ox بزاوية 90 درجة إلى شعاع Oy في اتجاه عقارب الساعة. في هذا الدليل نحن نحن نعتبر فقط أنظمة الإحداثيات اليمنى، دون أن يحدد ذلك على وجه التحديد.

إذا أدخلنا نظامًا من الإحداثيات الديكارتية المستطيلة أوكسي على المستوى، فستكتسب كل نقطة من المستوى إحداثيتين – الإحداثي السينيو تنسيق، والتي يتم حسابها على النحو التالي. دع A تكون نقطة تعسفية على المستوى. دعونا نسقط الخطوط المتعامدة من النقطة أ أ.أ. 1 و أ.أ. 2 إلى الخطوط المستقيمة الثور وأوي، على التوالي (الشكل 3).

التعريف 4. حدود النقطة A هي إحداثيات النقطة أ 1 على محور العدد ثور، إحداثي النقطة A هو إحداثي النقطة أ 2 على محور العدد أوي.

تعيين الإحداثيات (الإحداثيات والإحداثيات) للنقطةيُشار عادةً إلى A في نظام الإحداثيات الديكارتي المستطيل Oxy (الشكل 4). أ(س;ذ) أو أ = (س; ذ).

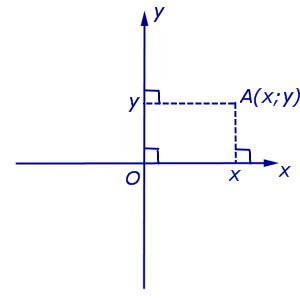
ملحوظة. النقطة O، تسمى أصل، لديها إحداثيات يا(0 ; 0) .

التعريف 5. في نظام الإحداثيات الديكارتي المستطيل Oxy، يُسمى المحور العددي Ox بالمحور الإحداثي، ويسمى المحور العددي Oy بالمحور الإحداثي (الشكل 5).

التعريف 6. يقسم كل نظام إحداثي ديكارتي مستطيل المستوى إلى أربعة أرباع (أرباع)، يظهر ترقيمها في الشكل 5.

التعريف 7. يسمى المستوى الذي يُعطى عليه نظام الإحداثيات الديكارتية المستطيل خطة تنسيق.

ملحوظة. يتم تحديد محور الإحداثيات على المستوى الإحداثي بواسطة المعادلة ذ= 0، يتم إعطاء المحور الإحداثي على المستوى الإحداثي بواسطة المعادلة س = 0.

البيان 1. المسافة بين نقطتينخطة تنسيق

أ 1 (س 1 ;ذ 1) و أ 2 (س 2 ;ذ 2)

محسوب وفقا للصيغة

دليل . النظر في الشكل 6.

|أ 1 أ 2 | 2 = = (س 2 -س 1) 2 + (ذ 2 -ذ 1) 2 .

(1)

لذلك،

Q.E.D.

معادلة الدائرة على المستوى الإحداثي

دعونا ننظر على المستوى الإحداثي أوكسي (الشكل 7) إلى دائرة نصف قطرها R ومركزها عند هذه النقطة أ 0 (س 0 ;ذ 0) .

في هذه المقالة سوف نقوم بتحليل تعريف دائرة الأعداد بتفصيل كبير، ومعرفة خصائصها الرئيسية وترتيب الأرقام 1،2،3، وما إلى ذلك. تعرف على كيفية وضع علامة على أرقام أخرى على دائرة (بما في ذلك pi).

دائرة الأرقام تسمى دائرة وحدة نصف القطر التي تتوافق نقاطها ، مرتبة وفق القواعد التالية:

1) نقطة الأصل في أقصى يمين الدائرة؛

2) عكس اتجاه عقارب الساعة - الاتجاه الإيجابي؛ في اتجاه عقارب الساعة - سلبي.

3) إذا رسمنا المسافة \(t\) على الدائرة في الاتجاه الموجب، فسنصل إلى نقطة قيمتها \(t\)؛

4) إذا رسمنا المسافة \(t\) على الدائرة في الاتجاه السلبي، فسنصل إلى نقطة قيمتها \(–t\).

لماذا سميت الدائرة بدائرة الأعداد؟
لأنه يحتوي على أرقام. بهذه الطريقة، تكون الدائرة مشابهة لمحور الأرقام - على الدائرة، كما هو الحال على المحور، هناك نقطة محددة لكل رقم.

لماذا تعرف ما هي دائرة الأرقام؟
باستخدام دائرة الأعداد، يتم تحديد قيم الجيب وجيب التمام والظل وظل التمام. لذلك، لمعرفة علم المثلثات واجتياز اختبار الدولة الموحدة بأكثر من 60 نقطة، يجب أن تفهم ما هي دائرة الأرقام وكيفية وضع النقاط عليها.

ماذا تعني عبارة "...من وحدة نصف القطر..." في التعريف؟
وهذا يعني أن نصف قطر هذه الدائرة يساوي \(1\). وإذا بنينا مثل هذه الدائرة التي مركزها نقطة الأصل فإنها ستتقاطع مع المحورين عند النقطتين \(1\) و\(-1\).

ليس من الضروري رسمها صغيرة، يمكنك تغيير "حجم" الأقسام على طول المحاور، ثم ستكون الصورة أكبر (انظر أدناه).

لماذا نصف القطر واحد بالضبط؟ وهذا أكثر ملاءمة، لأنه في هذه الحالة، عند حساب المحيط باستخدام الصيغة \(l=2πR\)، نحصل على:

طول دائرة الأعداد هو \(2π\) أو \(6.28\) تقريبًا.

ماذا يعني "... نقاطها تتوافق مع الأعداد الحقيقية"؟
كما قلنا أعلاه، في دائرة الأعداد لأي رقم حقيقي سيكون هناك بالتأكيد "مكانه" - النقطة التي تتوافق مع هذا الرقم.

لماذا تحديد الأصل والاتجاه على دائرة الأعداد؟
الغرض الرئيسي من دائرة الأرقام هو تحديد نقطتها لكل رقم بشكل فريد. ولكن كيف يمكنك تحديد مكان وضع النقطة إذا كنت لا تعرف من أين تعد ومن أين تتحرك؟

من المهم هنا عدم الخلط بين الأصل على خط الإحداثيات وعلى دائرة الأرقام - فهذان نظامان مرجعيان مختلفان! ولا تخلط أيضًا بين \(1\) على المحور \(x\) و\(0\) على الدائرة - فهذه نقاط على كائنات مختلفة.

ما هي النقاط التي تتوافق مع الأرقام \(1\) و\(2\) وما إلى ذلك؟
تذكر أننا افترضنا أن دائرة الأعداد يبلغ نصف قطرها \(1\)؟ ستكون هذه هي قطعة الوحدة الخاصة بنا (قياسًا على محور الأعداد)، والتي سنرسمها على الدائرة.

لتحديد نقطة على دائرة الأرقام المقابلة للرقم 1، عليك الانتقال من 0 إلى مسافة تساوي نصف القطر في الاتجاه الإيجابي.

لتحديد نقطة على الدائرة المقابلة للرقم \(2\)، تحتاج إلى قطع مسافة تساوي نصف قطرين من نقطة الأصل، بحيث يكون \(3\) مسافة تساوي ثلاثة أنصاف أقطار، وما إلى ذلك.

عند النظر إلى هذه الصورة، قد يكون لديك سؤالين:
1. ماذا يحدث عندما "تنتهي" الدائرة (أي نقوم بدورة كاملة)؟
الجواب: دعنا نذهب للجولة الثانية! وعندما ننتهي من الجزء الثاني، سننتقل إلى الجزء الثالث، وهكذا. ولذلك، يمكن رسم عدد لا حصر له من الأرقام على دائرة.

2. أين ستكون الأرقام السالبة؟
الجواب: هناك حق! ويمكن أيضًا ترتيبها عن طريق حساب العدد المطلوب من أنصاف الأقطار من الصفر، ولكن الآن في اتجاه سلبي.

لسوء الحظ، من الصعب الإشارة إلى الأعداد الصحيحة في دائرة الأعداد. ويرجع ذلك إلى حقيقة أن طول دائرة الأعداد لن يساوي عددًا صحيحًا: \(2π\). وفي الأماكن الأكثر ملائمة (عند نقاط التقاطع مع المحاور) سيكون هناك أيضًا كسور وليس أعداد صحيحة