ما هو مجموع زوايا متوازي الأضلاع؟ كيفية العثور على الزاوية الحادة لمتوازي الأضلاع

رباعيات.

§43. متوازي الاضلاع.

1. تعريف متوازي الأضلاع.

إذا قطعنا زوجًا من الخطوط المتوازية مع زوج آخر من الخطوط المتوازية، فسنحصل على شكل رباعي أضلاعه المتقابلة متوازية في أزواج.

في الرباعيات ABC و EFNM (الشكل 224) ВD || ايه سي و ايه بي || قرص مضغوط؛
إي أف || من و م || الجبهة الوطنية.

الشكل الرباعي الذي تكون أضلاعه المتقابلة متوازية في أزواج يسمى متوازي الأضلاع.

2. خصائص متوازي الأضلاع.

نظرية. قطر متوازي الأضلاع يقسمه إلى مثلثين متساويين.

يجب أن يكون هناك متوازي أضلاع ABC (الشكل 225)، حيث AB || سي دي و مكيف || في دي.

عليك أن تثبت أن القطر يقسمه إلى مثلثين متساويين.

دعونا نرسم القطر CB في متوازي الأضلاع ABC. دعونا نثبت ذلك /\ الكابينة = /\ سي دي في.

الجانب NE شائع في هذه المثلثات؛ / اي بي سي = / BCD، كزوايا عرضية داخلية متوازية AB وCD والقاطع CB؛ / ضياء = / СВD، يشبه أيضًا الزوايا المتقاطعة الداخلية مع التيار المتردد المتوازي و ВD والقاطع CB (الفقرة 38).

من هنا /\ الكابينة = /\ سي دي في.

وبنفس الطريقة، يمكن إثبات أن القطر AD سيقسم متوازي الأضلاع إلى مثلثين متساويين ACD وABD.

عواقب. 1 . الزوايا المتقابلة في متوازي الأضلاع متساوية مع بعضها البعض.

/ أ = / D، وهذا يتبع من مساواة المثلثين CAB وCDB.
على نفس المنوال / ج = / في.

2. عكس جوانب متوازية الأضلاعمتساوون مع بعضهم البعض.

AB = CD و AC = BD، حيث أن هذه الأضلاع مثلثات متساوية وتقع مقابل زوايا متساوية.

النظرية 2. تنقسم أقطار متوازي الأضلاع إلى نصفين عند نقطة تقاطعهما.

دع BC و AD هما قطرا متوازي الأضلاع ABC (الشكل 226). دعونا نثبت أن AO = OD و CO = OB.

للقيام بذلك، قارن بين زوج من المثلثات المتقابلة، على سبيل المثال /\ أوب و /\ سمك القد.

في هذه المثلثات AB = CD، مثل الجوانب المتقابلة لمتوازي الأضلاع؛
/ 1 = / 2، كزوايا داخلية تقع بالعرض مع التوازي AB وCD والقاطع AD؛
/ 3 = / 4 لنفس السبب، منذ AB || CD وCB هما قاطعاهما (§ 38).

إنه يتبع هذا /\ أوب = /\ سمك القد. و في مثلثات متساويةالجوانب المتساوية تقع مقابل زوايا متساوية. ولذلك، AO = OD وCO = OB.

النظرية 3. مجموع الزوايا المجاورة لأحد جانبي متوازي الأضلاع يساوي 2 د .

اثبات ذلك بنفسك.

3. علامات متوازي الأضلاع.

نظرية. إذا كانت الأضلاع المتقابلة في الشكل الرباعي متساوية في أزواج، فإن هذا الشكل الرباعي يكون متوازي أضلاع.

دعونا في الرباعي ABC (رسم 227) AB = CD وAC = BD. دعونا نثبت أنه في ظل هذا الشرط AB || سي دي و مكيف || ВD، أي أن الشكل الرباعي АВDC هو متوازي أضلاع.
دعونا نربط بقطعة بعض الرؤوس المتقابلة لهذا الشكل الرباعي، على سبيل المثال C و B. ينقسم الشكل الرباعي ABCD إلى مثلثين متساويين: /\ الكابينة و /\ سي دي في. في الواقع، لديهم نفس الجانب CB، AB = CD، وAC = BD وفقًا للحالة. وبالتالي، فإن ثلاثة أضلاع لمثلث واحد تساوي على التوالي ثلاثة أضلاع مثلث آخر /\ الكابينة = /\ سي دي في.

في المثلثات المتساوية، الزوايا المتساوية تقع مقابل جوانب متساوية، وبالتالي
/ 1 = / 2 و / 3 = / 4.

الزاويتان 1 و2 زاويتان داخليتان تقعان بالعرض عند تقاطع الخطين المستقيمين AB وCD للخط المستقيم CB. لذلك أ ب || قرص مضغوط.

وبنفس الطريقة، الزاويتان 3 و4 زاويتان داخليتان تقعان بالعرض عند تقاطع الخطين CA وBD للخط CB، وبالتالي CA || د (§ 35).

وبالتالي فإن الأضلاع المتقابلة في الشكل الرباعي ABCD متوازية في أزواج، وبالتالي فهو متوازي أضلاع، وهو ما يحتاج إلى إثبات.

النظرية 2. إذا كان هناك ضلعان متقابلان في شكل رباعي متساويان ومتوازيان، فإن الشكل الرباعي هو متوازي أضلاع.

دع AB = CD في الشكل الرباعي ABCD و AB || قرص مضغوط. دعونا نثبت أنه في ظل هذه الظروف يكون الشكل الرباعي ABC متوازي الأضلاع (الشكل 228).

دعونا نربط القمم C وB بالقطعة CB.نظرًا لتوازي الخطوط المستقيمة AB وCD، فإن الزاويتين 1 و2، كزاويتين داخليتين متقابلتين، متساويتان (الفقرة 38).
إذن المثلث CAB يساوي المثلث CDB، حيث أن لهما ضلع مشترك CB،
AB = CD حسب شروط النظرية و / 1 = / 2 بحسب ما ثبت. وتساوي هذه المثلثات يعني تساوي الزاويتين 3 و 4، حيث أنهما يقعان مقابل جوانب متساوية في مثلثات متساوية.

لكن الزاويتين 3 و 4 هما زاويتان عرضيتان داخليتان تتشكلان من تقاطع الخطين المستقيمين AC و BD للخط المستقيم CB، وبالتالي، AC || ВD (§ 35)، أي رباعي
ABC هو متوازي الأضلاع.

تمارين.

1. أثبت أنه إذا انقسمت أقطار الشكل الرباعي عند نقطة تقاطعهما إلى نصفين فإن هذا الرباعي يكون متوازي أضلاع.

2. إثبات أن الشكل الرباعي الذي مجموعه زوايا داخليةالمجاورة لكل ضلعين متجاورين تساوي 2 د، هناك متوازي الأضلاع.

3. أنشئ متوازي الأضلاع باستخدام الضلعين والزاوية بينهما:

أ) استخدام التوازي بين الجوانب المتقابلة لمتوازي الأضلاع؛
ب) استخدام تساوي الأضلاع المتقابلة في متوازي الأضلاع.

4. أنشئ متوازي الأضلاع باستخدام ضلعين متجاورين وقطريًا.

5. أنشئ متوازي الأضلاع باستخدام قطريه والزاوية بينهما.

6. أنشئ متوازي الأضلاع باستخدام ضلعه وقطريه.

متوازي الأضلاع هو شكل رباعي أضلاعه المتقابلة متوازية، أي. تقع على خطوط متوازية

خصائص متوازي الأضلاع: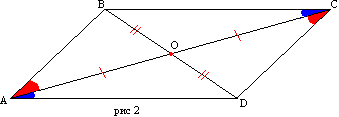
النظرية 22. الأضلاع المتقابلة في متوازي الأضلاع متساوية.
دليل. في متوازي الأضلاع ABCD، نرسم قطريًا AC. المثلثان ACD وACB متطابقان، إذ أن لهما جانبًا مشتركًا AC وزوجين من الزوايا المتساوية. المجاورة لها: ∠ CAB=∠ ACD، ∠ ACB=∠ DAC (كزوايا عرضية مع خطوط متوازية AD وBC). وهذا يعني أن AB = CD وBC = AD، كأضلاع متناظرة لمثلثات متساوية، وما إلى ذلك. ويترتب على تساوي هذه المثلثات أيضاً أن الزوايا المتناظرة في المثلثات متساوية:
النظرية 23. الزاويتان المتقابلتان في متوازي الأضلاع متساويتان: ∠ A=∠ C و ∠ B=∠ D.
مساواة الزوج الأول تأتي من مساواة المثلثات ABD وCBD، والثانية - ABC وACD.
النظرية 24. الزوايا المجاورة لمتوازي الأضلاع، أي. مجموع الزوايا المجاورة لجانب واحد يصل إلى 180 درجة.
وذلك لأنها زوايا داخلية أحادية الجانب.
النظرية 25. أقطار متوازي الأضلاع تنصف بعضها البعض عند نقطة تقاطعها.
دليل. خذ بعين الاعتبار المثلثين BOC وAOD. وفقًا للخاصية الأولى AD=BC ∠ OAD=∠ OCB و ∠ ODA=∠ OBC تقع بشكل عرضي للخطوط المتوازية AD وBC. ولذلك فإن المثلثين BOC وAOD متساويان في الزوايا الجانبية والمجاورة. وهذا يعني BO=OD وAO=OS، مثل الأضلاع المتناظرة في المثلثات المتساوية، وما إلى ذلك.

علامات متوازي الأضلاع
النظرية 26. إذا كانت الأضلاع المتقابلة في الشكل الرباعي متساوية في أزواج، فهو متوازي أضلاع.
دليل. دع الشكل الرباعي ABCD له جوانب AD وBC وAB وCD متساوية على التوالي (الشكل 2). دعونا نرسم التيار المتردد القطري. المثلثان ABC وACD متساويان من ثلاثة جوانب. إذن الزاويتان BAC وDCA متساويتان، وبالتالي فإن AB موازٍ للضلع CD. يأتي التوازي بين الجانبين BC وAD من تساوي الزوايا CAD وACB.
النظرية 27. لو زوايا متضادةالأشكال الرباعية متساوية في أزواج، فهي متوازي أضلاع.
دع ∠ A=∠ C و ∠ B=∠ D. لأن ∠ A+∠ B+∠ C+∠ D=360 o، ثم ∠ A+∠ B=180 o والضلعان AD وBC متوازيان (على أساس توازي الخطوط المستقيمة). وسنثبت أيضًا توازي الضلعين AB وCD، ونستنتج أن ABCD هو متوازي أضلاع بحكم التعريف.
النظرية 28. إذا كانت الزوايا المجاورة للشكل الرباعي، أي. مجموع الزوايا المجاورة لأحد الجانبين يصل إلى 180 درجة، فهو متوازي أضلاع.
إذا كان مجموع قياسات الزوايا الداخلية أحادية الجانب 180 درجة، فإن الخطوط المستقيمة متوازية. إذن AB يوازي CD وBC يوازي AD. تبين أن الشكل الرباعي هو متوازي أضلاع حسب التعريف.
النظرية 29. إذا كانت أقطار الشكل الرباعي تنصف بعضها البعض عند نقطة التقاطع، فإن الشكل الرباعي يكون متوازي أضلاع.
دليل. إذا كانت AO = OC، BO = OD، فإن المثلثين AOD وBOC متساويان، حيث أن لهما زوايا متساوية (عمودية) عند الرأس O، محاطة بين أزواج متساوية الجوانب. ومن تساوي المثلثين نستنتج أن AD وBC متساويان. الضلعان AB و CD متساويان أيضًا، ويتضح أن الشكل الرباعي متوازي أضلاع وفقًا للمعيار 1.
النظرية 30. إذا كان الشكل الرباعي يحتوي على زوج من الأضلاع المتساوية والمتوازية، فهو متوازي أضلاع.
اجعل الضلعين AB وCD للشكل الرباعي ABCD متوازيين ومتساويين. دعونا نرسم الأقطار AC و BD. ويترتب على توازي هذه الخطوط أن الزاويتين المتقاطعتين ABO = CDO و BAO = OCD متساويتان. المثلثان ABO وCDO متساويان في الزوايا الجانبية والمجاورة. ولذلك AO = OS، VO = ОD، أي. يتم تقسيم الأقطار إلى نصفين بنقطة التقاطع ويتضح أن الشكل الرباعي متوازي أضلاع حسب المعيار 4.

في الهندسة، يتم النظر في حالات خاصة لمتوازيات الأضلاع.

متوازي الأضلاع هو شكل رباعي أضلاعه المتقابلة متوازية، أي أنها تقع على خطوط متوازية (الشكل 1).

النظرية 1. حول خواص أضلاع وزوايا متوازي الأضلاع.في متوازي الأضلاع، الأضلاع المتقابلة متساوية، والزوايا المتقابلة متساوية، ومجموع الزوايا المجاورة لأحد جانبي متوازي الأضلاع هو 180 درجة.

دليل. في متوازي الأضلاع ABCD هذا، نرسم AC قطريًا ونحصل على مثلثين ABC وADC (الشكل 2).

هذه المثلثات متساوية، حيث أن ∠ 1 = ∠ 4، ∠ 2 = ∠ 3 (زوايا عرضية للخطوط المتوازية)، والجانب AC شائع. من المساواة Δ ABC = Δ ADC يترتب على ذلك أن AB = CD، BC = AD، ∠ B = ∠ D. مجموع الزوايا المجاورة لجانب واحد، على سبيل المثال الزاويتان A وD، يساوي 180 درجة كجانب واحد للخطوط المتوازية. لقد تم إثبات النظرية.

تعليق. إن تساوي الأضلاع المتقابلة في متوازي الأضلاع يعني أن أجزاء المتوازيات المقطوعة بأشكال متوازية متساوية.

النتيجة الطبيعية 1. إذا كان هناك خطان متوازيان، فإن جميع النقاط على خط واحد تكون على نفس المسافة من الخط الآخر.

دليل. بل دع || ب (الشكل 3).

دعونا نرسم عموديًا BA وCD على الخط المستقيم a من النقطتين B وC على الخط b. منذ أ ب || CD، فالشكل ABCD هو متوازي أضلاع، وبالتالي AB = CD.

المسافة بين خطين متوازيين هي المسافة من نقطة عشوائية على أحد الخطين إلى الخط الآخر.

وعلى ما ثبت فهو يساوي طول العمود المرسوم من نقطة ما لأحد المستقيمين المتوازيين إلى الخط الآخر.

مثال 1.محيط متوازي الأضلاع 122 سم، وأحد أضلاعه أكبر من الآخر بـ 25 سم، أوجد أضلاع متوازي الأضلاع.

حل. حسب النظرية 1، الأضلاع المتقابلة لمتوازي الأضلاع متساوية. دعنا نشير إلى أحد جانبي متوازي الأضلاع بـ x والآخر بـ y. ثم، حسب الشرط $$\left\(\begin(matrix) 2x + 2y = 122 \\x - y = 25 \end(matrix)\right.$$ وبحل هذا النظام، نحصل على x = 43، y = 18 وبذلك تكون أضلاع متوازي الأضلاع هي 18، 43، 18، 43 سم.

مثال 2.

حل. دع الشكل 4 يستوفي شروط المشكلة.

دعونا نرمز إلى AB بـ x، وBC بـ y. حسب الشرط، محيط متوازي الأضلاع هو 10 سم، أي 2(x + y) = 10، أو x + y = 5. محيط المثلث ABD هو 8 سم، وبما أن AB + AD = x + y = 5 إذن BD = 8 - 5 = 3. إذن BD = 3 سم.

مثال 3.أوجد زاويتي متوازي الأضلاع، مع العلم أن إحداهما أكبر من الأخرى بمقدار 50 درجة.

حل. دع الشكل 5 يستوفي شروط المشكلة.

دعونا نشير إلى قياس درجة الزاوية A بواسطة x. إذن قياس درجة الزاوية D هو x + 50°.

الزاويتان BAD وADC هما زاويتان داخليتان من جانب واحد مع خطوط متوازية AB وDC والقاطع AD. إذن مجموع هذه الزوايا المسماة سيكون 180 درجة، أي.
س + س + 50 درجة = 180 درجة، أو س = 65 درجة. وبالتالي، ∠ A = ∠ C = 65°، أ ∠ B = ∠ D = 115°.

مثال 4.جوانب متوازي الأضلاع هي 4.5 dm و 1.2 dm. يرسم المنصف من رأس زاوية حادة. ما الأجزاء التي يقسمها الجانب الأكبر من متوازي الأضلاع؟

حل. دع الشكل 6 يستوفي شروط المشكلة.

AE هو منصف الزاوية الحادة لمتوازي الأضلاع. ولذلك، ∠ 1 = ∠ 2.

المشكلة 1. قياس إحدى زوايا متوازي الأضلاع هو 65 درجة. أوجد الزوايا المتبقية في متوازي الأضلاع.

∠C =∠A = 65° زاويتان متقابلتان في متوازي الأضلاع.

∠A +∠B = 180° كزوايا مجاورة لأحد جوانب متوازي الأضلاع.

∠B = 180° - ∠A = 180° - 65° = 115°.

∠D =∠B = 115° هما الزاويتان المتقابلتان في متوازي الأضلاع.

الإجابة: ∠أ =∠C = 65°؛ ∠B =∠D = 115°.

المهمة 2.مجموع زاويتين في متوازي الأضلاع هو 220 درجة. أوجد زوايا متوازي الأضلاع.

بما أن متوازي الأضلاع به زاويتان متساويتان حادتان وزاويتان منفرجتان متساويتان، فإننا نحصل على مجموع زاويتين منفرجتين، أي. ∠B +∠D = 220°. ثم ∠B =∠D = 220° : 2 = 110°.

∠A + ∠B = 180° كزوايا مجاورة لجانب واحد من متوازي الأضلاع، لذا ∠A = 180° - ∠B = 180° - 110° = 70°. ثم ∠C =∠A = 70°.

الإجابة: ∠أ =∠C = 70°؛ ∠B =∠D = 110°.

المهمة 3.إحدى زوايا متوازي الأضلاع أكبر بثلاث مرات من الأخرى. أوجد زوايا متوازي الأضلاع.

دع ∠A =x. ثم ∠B = 3x. بمعرفة أن مجموع زوايا متوازي الأضلاع المجاورة لأحد أضلاعه هو 180 درجة، فإننا سننشئ معادلة.

س = 180 : 4;

نحصل على: ∠A = x = 45°، و∠B = 3x = 3 ∙ 45° = 135°.

الزوايا المتقابلة في متوازي الأضلاع متساوية، وبالتالي:

∠أ =∠C = 45°; ∠B =∠D = 135°.

الإجابة: ∠أ =∠C = 45°؛ ∠B =∠D = 135°.

المهمة 4.أثبت أنه إذا كان الشكل الرباعي له ضلعان متوازيان ومتساويان، فإن هذا الشكل الرباعي هو متوازي أضلاع.

دليل.

دعونا نرسم القطر BD ونفكر في Δ ADB و Δ CBD.

م = قبل الميلاد حسب الشرط. الجانب BD شائع. ∠1 = ∠2 كخط عرضي داخلي مع خطوط متوازية (حسب الحالة) AD وBC وsecant BD. لذلك، Δ ADB = Δ CBD على الجانبين والزاوية بينهما (العلامة الأولى لتساوي المثلثات). في المثلثات المتطابقة، الزوايا المتناظرة متساوية، وهو ما يعني ∠3 =∠4. وهذه الزوايا هي زوايا داخلية متعامدة مع الخطوط المستقيمة AB وCD والقاطع BD. وهذا يعني أن الخطين AB و CD متوازيان. وبالتالي، في هذا الشكل الرباعي ABCD، تكون الأضلاع المتقابلة متوازية في أزواج، وبالتالي، بحكم التعريف، ABCD هو متوازي أضلاع، وهو ما يجب إثباته.

المهمة 5.نسبة ضلعي متوازي الأضلاع هي 2 : 5، ومحيطه 3.5 م، أوجد أضلاع متوازي الأضلاع.

∙ (أ ب + م).

دعنا نشير إلى جزء واحد بواسطة x. ثم AB = 2x، AD = 5x متر. بمعرفة أن محيط متوازي الأضلاع هو 3.5 م، ننشئ المعادلة:

2 ∙ (2س + 5س) = 3.5؛

2 ∙ 7س = 3.5؛

س = 3.5 : 14;

جزء واحد طوله 0.25 م، ثم AB = 2 ∙ 0.25 = 0.5 م؛ م = 5 ∙ 0.25 = 1.25 م.

فحص.

محيط متوازي الأضلاع P ABCD = 2 ∙ (أ ب + م) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1.75 = 3.5 (م).

بما أن الأضلاع المتقابلة في متوازي الأضلاع متساوية، فإن CD = AB = 0.25 م؛ ق = م = 1.25 م.

الجواب: CD = AB = 0.25 م؛ ق = م = 1.25 م.

متوازي الأضلاع هو شكل رباعي تكون فيه الأضلاع المتقابلة متوازية في أزواج.

يحتوي متوازي الأضلاع على جميع خصائص الأشكال الرباعية، ولكنه بالإضافة إلى ذلك له أيضًا خصائصه الخاصة السمات المميزة. بمعرفتها، يمكننا بسهولة العثور على أضلاع وزوايا متوازي الأضلاع.

خصائص متوازي الأضلاع

1. مجموع الزوايا في أي متوازي أضلاع، كما هو الحال في أي شكل رباعي، هو 360 درجة.
2. تتقاطع الخطوط الوسطى لمتوازي الأضلاع وأقطاره عند نقطة واحدة وتنقسم بها. تسمى هذه النقطة عادةً بمركز تناظر متوازي الأضلاع.
3. الأضلاع المتقابلة لمتوازي الأضلاع تكون متساوية دائمًا.
4. كما أن هذا الشكل دائمًا له زوايا متقابلة متساوية.
5. مجموع الزوايا المجاورة لأي من أضلاع متوازي الأضلاع هو دائمًا 180 درجة.
6. مجموع مربعي قطري متوازي الأضلاع يساوي ضعف مجموع مربعي الضلعين المتجاورين. يتم التعبير عن ذلك بالصيغة:
   • d 1 2 + d 2 2 = 2 (a 2 + b 2)، حيث d 1 و d 2 قطران، a و b ضلعان متجاوران.
7. جيب تمام الزاوية المنفرجة يكون دائمًا أقل من الصفر.

كيف يمكن العثور على زوايا متوازي الأضلاع باستخدام هذه الخصائص عمليًا؟ وما هي الصيغ الأخرى التي يمكن أن تساعدنا في هذا؟ دعونا نلقي نظرة على المهام المحددة التي تتطلب: العثور على زوايا متوازي الأضلاع.

إيجاد زوايا متوازي الأضلاع

الحالة الأولى: قياس الزاوية المنفرجة معروف، وعلينا إيجاد زاوية حادة.

مثال: في متوازي الأضلاع ABCD، الزاوية A هي 120°. أوجد قياسات الزوايا المتبقية.

حل: باستخدام الخاصية رقم 5، يمكننا إيجاد قياس الزاوية B المجاورة للزاوية المعطاة في المهمة. سيكون مساوياً لـ:

• 180°-120°= 60°

والآن، باستخدام الخاصية رقم 4، نحدد أن الزاويتين المتبقيتين C وD متقابلتان للزوايا التي وجدناها بالفعل. الزاوية C معاكسة للزاوية A، والزاوية D معاكسة للزاوية B. وبالتالي فإنهما متساويان في أزواج.

• الإجابة: ب = 60 درجة، ج = 120 درجة، د = 60 درجة

الحالة الثانية: أطوال الأضلاع والأقطار معروفة

في هذه الحالة، علينا استخدام نظرية جيب التمام.

يمكننا أولًا حساب جيب تمام الزاوية التي نحتاجها باستخدام الصيغة، ثم استخدامها طاولة خاصةالعثور على ما تساوي الزاوية نفسها.

بالنسبة للزاوية الحادة الصيغة هي:

• cosa = (A² + B² - d²) / (2 * A * B)، حيث
• a هي الزاوية الحادة المطلوبة،
• A وB هما ضلعا متوازي الأضلاع،
• د - قطري أصغر

بالنسبة للزاوية المنفرجة، تتغير الصيغة قليلاً:

• cosß = (A² + B² - D²) / (2 * A * B)، حيث
• ß هي زاوية منفرجة،
• A وB هما الجانبين
• د - قطري كبير

مثال: أنت بحاجة إلى إيجاد زاوية حادة لمتوازي أضلاع طول ضلعيه 6 سم و 3 سم، والقطر الأصغر 5.2 سم

استبدل القيم في الصيغة لإيجاد زاوية حادة:

• cosa = (6 2 + 3 2 - 5.2 2) / (2 * 6 * 3) = (36 + 9 - 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
• كوزا = 1/2. ومن الجدول نستنتج أن الزاوية المطلوبة هي 60 درجة.