Cercul pe planul de coordonate. Lecție extracurriculară - cerc de numere

Destul de mult timp este dedicat cercului numeric în clasa a 10-a. Acest lucru se datorează semnificației acestui obiect matematic pentru întregul curs de matematică.

Mare valoare pentru buna absorbtie materialul are alegerea corectă a mijloacelor didactice. Cele mai eficiente astfel de instrumente includ tutoriale video. ÎN În ultima vreme ating apogeul popularității. Prin urmare, autorul nu a rămas în urmă vremurilor și a dezvoltat un manual atât de minunat pentru a ajuta profesorii de matematică - o lecție video pe tema „Cercul numeric pe planul de coordonate”.

Această lecție durează 15:22 minute. Este practic timp maxim pe care un profesor îl poate cheltui pentru a explica în mod independent materialul pe tema. Deoarece este nevoie de atât de mult timp pentru a explica materialul nou, este necesar să selectați cele mai eficiente sarcini și exerciții pentru consolidare și, de asemenea, să selectați o altă lecție în care elevii vor rezolva sarcini pe această temă.

Lecția începe cu o imagine a unui cerc numeric într-un sistem de coordonate. Autorul construiește acest cerc și își explică acțiunile. Apoi autorul numește punctele de intersecție ale cercului numeric cu axele de coordonate. În cele ce urmează se explică ce coordonate vor avea punctele cercului în diferite sferturi.

După aceasta, autorul ne reamintește cum arată ecuația unui cerc. Iar ascultătorilor li se prezintă două modele care înfățișează câteva puncte de pe cerc. Datorită acestui fapt, în pasul următor autorul arată cum să găsească coordonatele punctelor de pe cerc corespunzătoare anumitor numere marcate pe șabloane. Aceasta produce un tabel de valori pentru variabilele x și y din ecuația unui cerc.

În continuare, ne propunem să luăm în considerare un exemplu în care este necesar să se determine coordonatele punctelor dintr-un cerc. Înainte de a începe rezolvarea exemplului, se introduce o remarcă care ajută la rezolvarea acestuia. Și apoi pe ecran apare o soluție completă, clar structurată și ilustrată. Există și tabele aici care fac mai ușor de înțeles esența exemplului.

Apoi sunt luate în considerare încă șase exemple, care consumă mai puțin timp decât primul, dar nu mai puțin importante și reflectă ideea principală a lecției. Aici soluțiile sunt prezentate integral, cu o poveste detaliată și elemente de claritate. Și anume, soluția conține desene care ilustrează progresul soluției și o notație matematică care formează alfabetizarea matematică a elevilor.

Profesorul se poate limita la exemplele discutate în lecție, dar acest lucru poate să nu fie suficient pentru o învățare de înaltă calitate a materialului. Prin urmare, alegerea sarcinilor de consolidat este pur și simplu extrem de importantă.

Lecția poate fi utilă nu numai pentru profesori, al căror timp este limitat în mod constant, ci și pentru elevi. Mai ales pentru cei care primesc educație în familie sau se angajează în autoeducație. Materialele pot fi folosite de acei elevi care au ratat o lecție pe această temă.

DECODIFICAREA TEXTULUI:

Tema lecției noastre este „CERCUL NUMERIC PE PLAN DE COORDONATE”

Suntem deja familiarizați cu sistemul de coordonate dreptunghiular cartezian xOy (x o y). În acest sistem de coordonate vom plasa cerc numeric astfel încât centrul cercului să fie aliniat cu originea coordonatelor, iar raza acestuia este luată ca un segment de scară.

Punctul de pornire A al cercului numeric este combinat cu un punct cu coordonatele (1;0), B - cu un punct (0;1), C - cu (-1;0) (minus unu, zero) și D - cu (0; - 1)(zero, minus unu).

(vezi figura 1)

Deoarece fiecare punct al cercului numeric are propriile coordonate în sistemul xOy (x o y), atunci pentru punctele primului trimestru yx este mai mare decât zero și y este mai mare decât zero;

Al doilea trimestru ICH mai putin de zeroși jocul este mai mare decât zero,

pentru punctele din al treilea trimestru ikx este mai mic decât zero și yk este mai mic decât zero,

iar pentru al patrulea trimestru ikx este mai mare decât zero și yk este mai mic decât zero

Pentru orice punct E (x;y) (cu coordonatele x, y) al cercului numeric, inegalitățile -1≤ x≤ 1, -1≤y≤1 (x este mai mare sau egal cu minus unu, dar mai mic decât sau egal cu unu; y este mai mare sau egal cu minus unu, dar mai mic sau egal cu unu).

Reamintim că ecuația unui cerc de rază R cu centrul la origine are forma x 2 + y 2 = R 2 (x pătrat plus y pătrat este egal cu er pătrat). Și pentru cercul unitar R = 1, deci obținem x 2 + y 2 = 1

(x pătrat plus y pătrat este egal cu unu).

Să găsim coordonatele punctelor de pe cercul numeric, care sunt prezentate pe două scheme (vezi Fig. 2, 3)

Fie punctul E, care îi corespunde

(pi cu patru) - mijlocul primului trimestru prezentat în figură. Din punctul E coborâm perpendiculara EK pe dreapta OA și considerăm triunghiul OEK. Unghiul AOE =45 0, deoarece arcul AE este jumătate din arcul AB. Prin urmare, triunghiul OEK este un triunghi dreptunghic isoscel, pentru care OK = EC. Aceasta înseamnă că abscisa și ordonata punctului E sunt egale, adică. x este egal cu jocul. Pentru a găsi coordonatele punctului E, rezolvăm sistemul de ecuații: (x este egal cu y - prima ecuație a sistemului și x pătrat plus y pătrat este egal cu unu - a doua ecuație a sistemului). ecuația sistemului, în loc de x, înlocuim y, obținem 2y 2 = 1 (două y pătrat este egal cu unu), de unde y = = (y este egal cu unul împărțit la rădăcina a doi este egal cu rădăcina a doi împărțită la doi) (ordonata este pozitivă) Aceasta înseamnă că punctul E din sistemul de coordonate dreptunghiular are coordonatele (,) (rădăcina a doi împărțită la doi, rădăcina a doi împărțită la doi).

Raționând într-un mod similar, găsim coordonatele punctelor corespunzătoare altor numere din primul aspect și obținem: punctul corespunzător este cu coordonatele (- ,) (minus rădăcina a doi împărțită la doi, rădăcina a doi împărțită la doi) ; pentru - (- ,-) (minus rădăcina a doi împărțit la doi, minus rădăcina a doi împărțit la doi); pentru (șapte pi peste patru) (,)(rădăcina doi împărțit la doi, minus rădăcina doi împărțit la doi).

Fie punctul D să corespundă cu (Fig. 5). Să lăsăm perpendiculara de la DP(de pe) la OA și să luăm în considerare triunghiul ODP. Ipotenuza acestui triunghi OD este egală cu raza cercului unitar, adică unu, iar unghiul DOP este egal cu treizeci de grade, deoarece arcul AD = digi AB (a de este egal cu o treime a be), și arcul AB este egal cu nouăzeci de grade. Prin urmare, DP = (de pe este egal cu o jumătate O de este egal cu o jumătate) Deoarece piciorul situat opus unghiului de treizeci de grade este egal cu jumătate din ipotenuză, adică y = (y este egal cu o jumătate) . Aplicând teorema lui Pitagora, obținem OR 2 = OD 2 - DP 2 (o pe pătrat este egal cu o de pătrat minus de pe pătrat), dar OR = x (o pe este egal cu x). Aceasta înseamnă x 2 = OD 2 - DP 2 =

aceasta înseamnă x 2 = (x pătrat este egal cu trei sferturi) și x = (x este egal cu rădăcina de trei ori doi).

X este pozitiv, deoarece este in primul trimestru. Am descoperit că punctul D dintr-un sistem de coordonate dreptunghiular are coordonatele (,) rădăcină a lui trei împărțite la doi, o jumătate.

Raționând într-un mod similar, vom găsi coordonatele punctelor corespunzătoare altor numere ale celui de-al doilea aspect și vom scrie toate datele obținute în tabele:

Să ne uităm la exemple.

EXEMPLUL 1. Aflați coordonatele punctelor de pe cercul numeric: a) C 1 ();

b) C2 (); c) C3 (41π); d) C4 (- 26π). (tse unu corespunzând la treizeci și cinci pi cu patru, tse doi corespunzând minus patruzeci și nouă pi cu trei, tse trei corespunzând la patruzeci și unu pi, tse patru corespunzând minus douăzeci și șase pi).

Soluţie. Să folosim afirmația obținută mai devreme: dacă punctul D al cercului numeric corespunde numărului t, atunci acesta corespunde oricărui număr de forma t + 2πk(te plus două vârfuri), unde ka este orice număr întreg, adică. kϵZ (ka aparține lui z).

a) Se obține = ∙ π = (8 +) ∙π = + 2π ∙ 4. (treizeci și cinci pi ori patru este egal cu treizeci și cinci ori patru, înmulțit cu pi este egal cu suma de opt și trei sferturi, înmulțit cu pi este egal trei pi cu patru plus produsul a doi pi cu patru).Aceasta înseamnă că numărul treizeci și cinci pi cu patru corespunde aceluiași punct din cercul numeric ca și numărul trei pi cu patru. Folosind Tabelul 1, obținem C 1 () = C 1 (- ;) .

b) Similar cu coordonatele C 2: = ∙ π = - (16 + ∙π = + 2π ∙ (- 8). Aceasta înseamnă că numărul

corespunde aceluiași punct de pe cercul numeric cu numărul. Și numărul corespunde aceluiași punct de pe cercul numeric ca și numărul

(afișați al doilea aspect și tabelul 2). Pentru un punct avem x = , y =.

c) 41π = 40π + π = π + 2π ∙ 20. Aceasta înseamnă că numărul 41π corespunde aceluiași punct de pe cercul numeric ca și numărul π - acesta este un punct cu coordonate (-1; 0).

d) - 26π = 0 + 2π ∙ (- 13), adică numărul - 26π corespunde aceluiași punct de pe cercul numeric ca și numărul zero - acesta este un punct cu coordonate (1;0).

EXEMPLU 2. Găsiți puncte pe cercul numeric cu ordonată y =

Soluţie. Linia dreaptă y = intersectează cercul numeric în două puncte. Un punct corespunde unui număr, al doilea punct corespunde unui număr,

Prin urmare, obținem toate punctele adăugând o revoluție completă 2πk unde k arată câte rotații complete face punctul, adică. primim,

iar pentru orice număr toate numerele de forma + 2πk. Adesea în astfel de cazuri ei spun că au primit două serii de valori: + 2πk, + 2πk.

EXEMPLU 3. Găsiți puncte pe cercul numeric cu abscisă x = și notați căror numere t corespund.

Soluţie. Drept X= intersectează cercul numeric în două puncte. Un punct corespunde unui număr (vezi al doilea aspect),

și deci orice număr de forma + 2πk. Iar al doilea punct corespunde unui număr și, prin urmare, oricărui număr de forma + 2πk. Aceste două serii de valori pot fi acoperite într-o singură intrare: ± + 2πk (plus minus doi pi cu trei plus doi pi).

EXEMPLU 4. Găsiți puncte cu ordonată pe cercul numeric la> și notează căror numere t corespund.

Linia dreaptă y = intersectează cercul numeric în două puncte M și P. Și inegalitatea y > corespunde punctelor arcului deschis MR, aceasta înseamnă arce fără capete (adică fără u), când se deplasează în jurul cercului în sens invers acelor de ceasornic. , începând din punctul M și terminând în punctul P. Aceasta înseamnă că nucleul notației analitice a arcului MR este inegalitatea< t < (тэ больше, чем пи на три, но меньше двух пи на три) , а сама аналитическая запись дуги имеет вид + 2πk < t < + 2πk(тэ больше, чем пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).

EXEMPLUL5. Găsiți punctele ordonate pe cercul numeric la < и записать, каким числам t они соответствуют.

Linia dreaptă y = intersectează cercul numeric în două puncte M și P. Și inegalitatea y< соответствуют точки открытой дуги РМ при движении по окружности против часовой стрелки, начиная с точки Р, а заканчивая в точке М. Значит, ядром аналитической записи дуги РМ является неравенство < t < (тэ больше, чем минус четыре пи на три, но меньше пи на три) , а сама аналитическая запись дуги имеет вид

2πk< t < + 2πk (тэ больше, чем минус четыре пи на три плюс два пи ка, но меньше пи на три плюс два пи ка).

EXEMPLU 6. Găsiți puncte cu abscisă pe cercul numeric X> și notează căror numere t corespund.

Linia dreaptă x = intersectează cercul numeric în două puncte M și P. Inegalitatea x > corespunde punctelor arcului deschis PM atunci când se deplasează de-a lungul cercului în sens invers acelor de ceasornic cu începutul în punctul P, care corespunde, și sfârșitul în punctul M, care corespunde. Aceasta înseamnă că nucleul notației analitice a arcului PM este inegalitatea< t <

(te este mai mare decât minus doi pi pe trei, dar mai mic de doi pi pe trei), iar notația analitică a arcului în sine are forma + 2πk< t < + 2πk (тэ больше, чем минус два пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).

EXEMPLU 7. Găsiți puncte cu abscisă pe cercul numeric X < и записать, каким числам t они соответствуют.

Linia dreaptă x = intersectează cercul numeric în două puncte M și P. Inegalitatea x< соответствуют точки открытой дуги МР при движении по окружности против часовой стрелки с началом в точке М, которая соответствует, и концом в точке Р, которая соответствует. Значит, ядром аналитической записи дуги МР является неравенство < t <

(te este mai mult de doi pi pe trei, dar mai mic de patru pi pe trei), iar notația analitică a arcului în sine are forma + 2πk< t < + 2πk (тэ больше, чем два пи на три плюс два пи ка, но меньше четырех пи на три плюс два пи ка).

Cercul numeric este un cerc unitar ale cărui puncte corespund unor numere reale.

Un cerc unitar este un cerc cu raza 1.

Vedere generală a cercului numeric.

1) Raza sa este luată ca unitate de măsură.

2) Diametrele orizontale și verticale împart cercul numeric în patru sferturi (vezi figura). Ele sunt numite, respectiv, primul, al doilea, al treilea și al patrulea trimestru.

3) Diametrul orizontal este notat cu AC, cu A fiind punctul extrem din dreapta.
Diametrul vertical este desemnat BD, cu B fiind punctul cel mai înalt.
Respectiv:

primul sfert este arcul AB

al doilea sfert – arc BC

al treilea sfert – arc CD

al patrulea sfert – arc DA

4) Punctul de pornire al cercului numeric este punctul A.

Numărarea de-a lungul cercului numeric se poate face fie în sensul acelor de ceasornic, fie în sens invers acelor de ceasornic.
Numărarea din punctul A se numește în sens invers acelor de ceasornic direcție pozitivă.
Se numește numărătoarea din punctul A în sensul acelor de ceasornic direcție negativă.

Cercul numeric pe planul de coordonate.

Centrul razei cercului numeric corespunde originii (numărul 0).

Diametrul orizontal corespunde axei X, verticale – axe y.

Punctul de pornire A al cercului numeric este pe axă Xși are coordonatele (1; 0).

ValoriXȘiyîn sferturi de cerc numeric:

Valorile de bază ale cercului numeric:

Numele și locațiile principalelor puncte de pe cercul numeric:

Cum să vă amintiți numele cercurilor numerice.

Există mai multe modele simple care vă vor ajuta să vă amintiți cu ușurință numele de bază ale cercului numeric.

Înainte de a începe, permiteți-ne să vă reamintim: numărarea se efectuează în sens pozitiv, adică din punctul A (2π) în sens invers acelor de ceasornic.

1) Să începem cu punctele extreme de pe axele de coordonate.

Punctul de pornire este 2π (punctul cel mai din dreapta pe axă X, egal cu 1).

După cum știți, 2π este circumferința unui cerc. Aceasta înseamnă că o jumătate de cerc este 1π sau π. Axă Xîmparte cercul exact în jumătate. În consecință, punctul cel mai din stânga pe axă X egal cu -1 se numește π.

Cel mai înalt punct de pe axă la, egal cu 1, împarte semicercul superior în jumătate. Aceasta înseamnă că dacă un semicerc este π, atunci jumătate de semicerc este π/2.

În același timp, π/2 este și un sfert de cerc. Să numărăm trei astfel de sferturi de la primul la al treilea - și vom ajunge la punctul cel mai de jos al axei la, egal cu -1. Dar dacă include trei sferturi, atunci numele său este 3π/2.

2) Acum să trecem la punctele rămase. Vă rugăm să rețineți: toate punctele opuse au același numărător - și acestea sunt puncte opuse față de axă la, atât relativ la centrul axelor, cât și relativ la axă X. Acest lucru ne va ajuta să le cunoaștem valorile punctuale fără a înghesui.

Trebuie doar să vă amintiți semnificația punctelor din primul trimestru: π/6, π/4 și π/3. Și apoi vom „vedea” câteva modele:

- Raportat la axa yîn punctele celui de-al doilea trimestru, opus punctelor primului trimestru, numerele din numărători sunt cu 1 mai mici decât mărimea numitorilor. De exemplu, luați punctul π/6. Punctul opus acestuia în raport cu axa la are de asemenea 6 la numitor și 5 la numărător (1 mai puțin). Adică numele acestui punct este: 5π/6. Punctul opus lui π/4 are și 4 la numitor și 3 la numărător (1 mai mic decât 4) - adică este un punct 3π/4.
Punctul opus lui π/3 are și 3 la numitor și 1 mai puțin la numărător: 2π/3.

- Raportat la centrul axelor de coordonate totul este invers: numerele din numărătorii punctelor opuse (în al treilea trimestru) sunt cu 1 mai mari decât valoarea numitorilor. Să luăm din nou punctul π/6. Punctul opus acestuia față de centru are și 6 la numitor, iar la numărător numărul este cu 1 mai mare - adică este 7π/6.

Punctul opus punctului π/4 are și el 4 la numitor, iar la numărător numărul este cu 1 mai mult: 5π/4.
Punctul opus punctului π/3 are și el 3 la numitor, iar la numărător numărul este cu 1 mai mult: 4π/3.

- Relativ la axa X(al patrulea sfert) treaba este mai complicata. Aici trebuie să adăugați la valoarea numitorului un număr care este cu 1 mai mic - această sumă va fi egală cu partea numerică a numărătorului punctului opus. Să începem din nou cu π/6. Să adăugăm la valoarea numitorului egală cu 6 un număr care este cu 1 mai mic decât acest număr - adică 5. Se obține: 6 + 5 = 11. Aceasta înseamnă că este opus axei X punctul va avea 6 la numitor și 11 la numărător - adică 11π/6.

Punctul π/4. Adăugăm la valoarea numitorului un număr cu 1 mai mic: 4 + 3 = 7. Aceasta înseamnă că este opus axei X punctul are 4 la numitor și 7 la numărător - adică 7π/4.
Punctul π/3. Numitorul este 3. Adăugăm la 3 un număr mai mic cu unu - adică 2. Obținem 5. Aceasta înseamnă că punctul opus are 5 la numărător - și acesta este punctul 5π/3.

3) Un alt model pentru punctele punctelor mijlocii ale sferturilor. Este clar că numitorul lor este 4. Să fim atenți la numărători. Numătorul mijlocului primului trimestru este 1π (dar nu este obișnuit să scrieți 1). Numătorul mijlocului celui de-al doilea trimestru este 3π. Numătorul mijlocului celui de-al treilea trimestru este 5π. Numătorul mijlocului celui de-al patrulea trimestru este 7π. Se pare că numărătorii sferturilor din mijloc conțin primele patru numere impare în ordine crescătoare:
(1)π, 3π, 5π, 7π.
Acest lucru este, de asemenea, foarte simplu. Deoarece punctele de mijloc ale tuturor sferturilor au 4 la numitor, știm deja numele lor complete: π/4, 3π/4, 5π/4, 7π/4.

Caracteristicile cercului numeric. Comparație cu dreapta numerică.

După cum știți, pe linia numerică, fiecărui punct îi corespunde un singur număr. De exemplu, dacă punctul A de pe o linie este egal cu 3, atunci nu mai poate fi egal cu niciun alt număr.

Este diferit pe cercul numeric pentru că este un cerc. De exemplu, pentru a ajunge de la punctul A al unui cerc la punctul M, o puteți face ca pe o linie dreaptă (trecând doar un arc), sau puteți ocoli un întreg cerc și apoi ajungeți la punctul M. Concluzie:

Fie punctul M egal cu un număr t. După cum știm, circumferința unui cerc este 2π. Aceasta înseamnă că putem scrie un punct pe un cerc t în două moduri: t sau t + 2π. Acestea sunt valori echivalente.
Adică t = t + 2π. Singura diferență este că în primul caz ați ajuns imediat la punctul M fără a face un cerc, iar în al doilea caz ați făcut un cerc, dar ați ajuns în același punct M. Puteți face două, trei sau două sute de astfel de cercuri . Dacă notăm numărul de cercuri prin literă k, atunci obținem o nouă expresie:
t = t + 2π k.

De aici formula:

Ecuația cercului numeric
(a doua ecuație este în secțiunea „Sinus, cosinus, tangent, cotangent”):

x 2 + y 2 = 1

Vă prezentăm atenției o lecție video pe tema „Cercul numărului”. Se oferă o definiție a ceea ce sunt sinusul, cosinusul, tangenta, cotangenta și funcțiile y= păcat X, y= cos X, y= tg X, y= ctg X pentru orice argument numeric. Luăm în considerare problemele standard de corespondență între numere și puncte din cercul numărului unitar pentru a găsi un singur punct pentru fiecare număr și, invers, pentru a găsi pentru fiecare punct o mulțime de numere care îi corespunde.

Tema: Elemente de teoria funcţiilor trigonometrice

Lecția: Cercul numerelor

Scopul nostru imediat este definirea funcțiilor trigonometrice: sinusurilor, cosinus, tangentă, cotangentă-

Argumentul numeric poate fi trasat pe o linie de coordonate sau pe un cerc.

Un astfel de cerc se numește cerc numeric sau unitar, deoarece pentru comoditate, faceți un cerc cu

De exemplu, dat un punct, marcați-l pe linia de coordonate

și pe cerc numeric.

Când lucrați cu cercul numeric, sa convenit că mișcarea în sens invers acelor de ceasornic este o direcție pozitivă, în sensul acelor de ceasornic este o direcție negativă.

Sarcini tipice - trebuie să determinați coordonatele unui punct dat sau, dimpotrivă, să găsiți un punct după coordonatele sale.

Linia de coordonate stabilește o corespondență unu-la-unu între puncte și numere. De exemplu, un număr corespunde punctului A cu coordonate

Fiecare punct B cu o coordonată este caracterizat de un singur număr - distanța de la 0 la luată cu semnul plus sau minus.

Pe cercul numeric, corespondența unu-la-unu funcționează doar într-o singură direcție.

De exemplu, există un punct B pe cercul de coordonate (Fig. 2), lungimea arcului este 1, adică. acest punct corespunde cu 1.

Dat un cerc, lungimea cercului Dacă atunci este lungimea cercului unitar.

Dacă adunăm , obținem același punct B, atunci ajungem și la punctul B, scădem - și punctul B.

Luați în considerare punctul B: lungimea arcului = 1, apoi numerele caracterizează punctul B pe cercul numeric.

Astfel, numărul 1 corespunde unui singur punct de pe cercul numeric - punctul B, iar punctul B corespunde unui număr infinit de puncte de forma .

Următoarele sunt valabile pentru cercul numeric:

Dacă T. M Dacă cercul numeric corespunde unui număr, atunci acesta corespunde și unui număr din formă

Puteți face câte rotații complete în jurul cercului numeric doriți, într-o direcție pozitivă sau negativă - punctul este același. Prin urmare, ecuațiile trigonometrice au un număr infinit de soluții.

De exemplu, dat punctul D. Care sunt numerele cărora le corespunde?

Măsurăm arcul.

mulţimea tuturor numerelor corespunzătoare punctului D.

Să ne uităm la punctele principale ale cercului numeric.

Lungimea întregii circumferințe.

Acestea. înregistrarea mai multor coordonate poate fi diferită .

Să ne uităm la problemele tipice ale cercului numeric.

1. Având în vedere: . Găsiți: un punct pe cercul numeric.

Să selectăm întreaga parte:

Este necesar să găsiți punctul pe cercul numeric. , Apoi .

Acest set include și punctul.

2. Având în vedere: . Găsiți: un punct pe cercul numeric.

Este necesar să se găsească t.

t.aparține și acestui set.

Rezolvând probleme standard de corespondență între numere și puncte de pe cercul numeric, am aflat că pentru fiecare număr putem găsi un singur punct, iar pentru fiecare punct putem găsi o mulțime de numere care sunt caracterizate de un punct dat.

Împărțiți arcul în trei părți egale și marcați punctele M și N.

Să găsim toate coordonatele acestor puncte.

Deci, scopul nostru este să definim funcții trigonometrice. Pentru a face acest lucru, trebuie să învățăm cum să specificăm un argument de funcție. Ne-am uitat la punctele cercului unitar și am rezolvat două probleme tipice - găsirea unui punct pe cercul numeric și notarea tuturor coordonatele punctului pe cercul unității.

1. Mordkovich A.G. si altele.Algebra Clasa a IX-a: Manual. Pentru invatamantul general Instituții.- Ed. a IV-a. - M.: Mnemosyne, 2002.-192 p.: ill.

2. Mordkovich A.G. și altele.Algebră Clasa a IX-a: Cartea de probleme pentru studenții instituțiilor de învățământ general / A. G. Mordkovich, T. N. Mishustina etc.- ed. a IV-a. - M.: Mnemosyne, 2002.-143 p.: ill.

3. Makarychev Yu. N. Algebră. Clasa a IX-a: educațional pentru elevii din învățământul general. instituții / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, I. E. Feoktistov. — Ed. a VII-a, rev. si suplimentare - M.: Mnemosyne, 2008.

4. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. Algebră. clasa a 9-a. a 16-a ed. - M., 2011. - 287 p.

5. Mordkovich A. G. Algebră. clasa a 9-a. În 2 ore Partea 1. Manual pentru studenții instituțiilor de învățământ general / A. G. Mordkovich, P. V. Semenov. — Ed. a XII-a, șters. - M.: 2010. - 224 p.: ill.

6. Algebră. clasa a 9-a. În 2 părți Partea 2. Cartea cu probleme pentru studenții instituțiilor de învățământ general / A. G. Mordkovich, L. A. Aleksandrova, T. N. Mishustina și alții; Ed. A. G. Mordkovici. — Ed. a XII-a, rev. - M.: 2010.-223 p.: ill.

Mordkovich A.G. și altele.Algebră Clasa a IX-a: Cartea de probleme pentru studenții instituțiilor de învățământ general / A. G. Mordkovich, T. N. Mishustina etc.- ed. a IV-a. - M.: Mnemosyne, 2002.-143 p.: ill.

№№ 531; 536; 537; 541; 552.

Ecuația unui cerc pe planul de coordonate

Definiția 1. Axa numerelor ( linie numerică, linie de coordonate) Ox este linia dreaptă pe care este selectat punctul O origine (originea coordonatelor)(Fig.1), direcție

O → X

enumerate ca direcție pozitivăși se marchează un segment, a cărui lungime se consideră a fi unitate de lungime.

Definiția 2. Un segment a cărui lungime este luată ca unitate de lungime se numește scară.

Fiecare punct de pe axa numerelor are o coordonată care este un număr real. Coordonata punctului O este zero. Coordonata unui punct arbitrar A situat pe raza Ox este egală cu lungimea segmentului OA. Coordonata unui punct arbitrar A al axei numerice care nu se află pe raza Ox este negativă, iar în valoare absolută este egală cu lungimea segmentului OA.

Definiția 3. Sistemul de coordonate carteziene dreptunghiulare Oxy pe plan sunați doi reciproc perpendicular axele numerice Ox si Oy cu aceeasi scaraȘi punct de referință comunîn punctul O și astfel încât rotația de la raza Ox la un unghi de 90° la raza Oy se efectuează în direcția în sens invers acelor de ceasornic(Fig. 2).

Notă. Sistemul de coordonate carteziene dreptunghiulare Oxy, prezentat în figura 2, se numește sistemul de coordonate corect, Spre deosebire de sisteme de coordonate stânga, în care rotirea fasciculului Ox la un unghi de 90° față de fasciculul Oy se realizează în sensul acelor de ceasornic. În acest ghid noi considerăm doar sisteme de coordonate drepte, fără a o specifica în mod specific.

Dacă introducem un sistem de coordonate carteziene dreptunghiulare Oxy pe plan, atunci fiecare punct al planului va dobândi două coordonate – abscisăȘi ordonată, care se calculează după cum urmează. Fie A un punct arbitrar pe plan. Să lăsăm perpendicularele din punctul A A.A. 1 și A.A. 2 la liniile drepte Ox și, respectiv, Oy (Fig. 3).

Definiția 4. Abscisa punctului A este coordonata punctului A 1 pe axa numerelor Ox, ordonata punctului A este coordonata punctului A 2 pe axa numerelor Oy.

Desemnare Coordonatele (abscisa si ordonata) punctului A în sistemul de coordonate carteziene dreptunghiulare Oxy (Fig. 4) este de obicei notat A(X;y) sau A = (X; y).

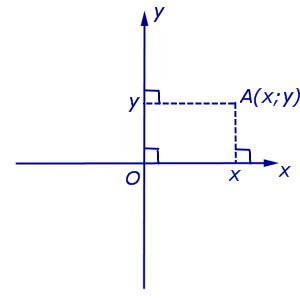
Notă. Punctul O, numit origine, are coordonate O(0 ; 0) .

Definiția 5. În sistemul de coordonate carteziene dreptunghiulare Oxy, axa numerică Ox se numește axa absciselor, iar axa numerică Oy se numește axa ordonatelor (Fig. 5).

Definiția 6. Fiecare sistem de coordonate carteziene dreptunghiulare împarte planul în 4 sferturi (cadrante), a căror numerotare este prezentată în Figura 5.

Definiția 7. Se numește planul pe care este dat un sistem de coordonate carteziene dreptunghiulare plan de coordonate.

Notă. Axa absciselor este specificată pe planul de coordonate prin ecuație y= 0, axa ordonatelor este dată pe planul de coordonate de ecuație X = 0.

Afirmația 1. Distanța dintre două puncte plan de coordonate

A 1 (X 1 ;y 1) Și A 2 (X 2 ;y 2)

calculat conform formulei

Dovada . Luați în considerare figura 6.

|A 1 A 2 | 2 = = (X 2 -X 1) 2 + (y 2 -y 1) 2 .

(1)

Prin urmare,

Q.E.D.

Ecuația unui cerc pe planul de coordonate

Să considerăm pe planul de coordonate Oxy (Fig. 7) un cerc de rază R cu centru în punctul A 0 (X 0 ;y 0) .

În acest articol vom analiza în detaliu definiția cercului numeric, vom afla proprietatea sa principală și vom aranja numerele 1,2,3 etc. Aflați cum să marcați alte numere pe un cerc (inclusiv pi).

Cercul numeric numit cerc cu raza unitară ale cărui puncte corespund , aranjate după următoarele reguli:

1) Originea este în punctul extrem drept al cercului;

2) În sens invers acelor de ceasornic - sens pozitiv; în sensul acelor de ceasornic – negativ;

3) Dacă trasăm distanța \(t\) pe cerc în direcția pozitivă, atunci vom ajunge la un punct cu valoarea \(t\);

4) Dacă trasăm distanța \(t\) pe cerc în direcția negativă, atunci vom ajunge la un punct cu valoarea \(–t\).

De ce se numește cercul cerc numeric?
Pentru că are numere pe el. În acest fel, cercul este similar cu axa numerelor - pe cerc, ca și pe axă, există un punct specific pentru fiecare număr.

De ce știi ce este un cerc numeric?
Folosind cercul numeric, se determină valorile sinusurilor, cosinusurilor, tangentelor și cotangentelor. Prin urmare, pentru a cunoaște trigonometria și pentru a promova examenul de stat unificat cu peste 60 de puncte, trebuie să înțelegeți ce este un cerc numeric și cum să plasați puncte pe el.

Ce înseamnă cuvintele „...de raza unității...” în definiție?
Aceasta înseamnă că raza acestui cerc este egală cu \(1\). Și dacă construim un astfel de cerc cu centrul la origine, atunci se va intersecta cu axele în punctele \(1\) și \(-1\).

Nu trebuie să fie desenat mic; puteți modifica „dimensiunea” diviziunilor de-a lungul axelor, apoi imaginea va fi mai mare (vezi mai jos).

De ce raza este exact una? Acest lucru este mai convenabil, deoarece în acest caz, când se calculează circumferința folosind formula \(l=2πR\), obținem:

Lungimea cercului numeric este \(2π\) sau aproximativ \(6,28\).

Ce înseamnă „... ale căror puncte corespund numerelor reale”?
După cum am spus mai sus, pe cercul numeric pentru orice număr real va exista cu siguranță „locul” acestuia - un punct care corespunde acestui număr.

De ce să se determine originea și direcția pe cercul numeric?
Scopul principal al cercului numeric este de a determina în mod unic punctul său pentru fiecare număr. Dar cum puteți determina unde să puneți punctul dacă nu știți de unde să numărați și unde să vă mutați?

Aici este important să nu confundați originea pe linia de coordonate și pe cercul numeric - acestea sunt două sisteme de referință diferite! Și, de asemenea, nu confundați \(1\) pe axa \(x\) și \(0\) pe cerc - acestea sunt puncte pe diferite obiecte.

Care puncte corespund numerelor \(1\), \(2\), etc.?
Amintiți-vă, am presupus că cercul numeric are o rază de \(1\)? Acesta va fi segmentul nostru unitar (prin analogie cu axa numerelor), pe care îl vom reprezenta pe cerc.

Pentru a marca un punct pe cercul numeric corespunzător numărului 1, trebuie să mergeți de la 0 la o distanță egală cu raza în direcția pozitivă.

Pentru a marca un punct pe cerc corespunzător numărului \(2\), trebuie să parcurgeți o distanță egală cu două raze de la origine, astfel încât \(3\) să fie o distanță egală cu trei raze etc.

Când vă uitați la această imagine, este posibil să aveți 2 întrebări:
1. Ce se întâmplă când cercul „se termină” (adică facem o revoluție completă)?
Răspuns: să trecem la turul doi! Și când se termină al doilea, vom merge la al treilea și așa mai departe. Prin urmare, un număr infinit de numere poate fi trasat pe un cerc.

2. Unde vor fi numerele negative?
Răspuns: chiar acolo! Ele pot fi, de asemenea, aranjate, numărând de la zero numărul necesar de raze, dar acum în direcție negativă.

Din păcate, este dificil să notezi numere întregi pe cercul numeric. Acest lucru se datorează faptului că lungimea cercului numeric nu va fi egală cu un număr întreg: \(2π\). Și în locurile cele mai convenabile (în punctele de intersecție cu axele) vor exista și fracții, nu numere întregi