מהו סכום כל הזוויות של מקבילית. כיצד למצוא את הזווית החדה של מקבילית

27.09.2019

QUADAGONS.

§43. מַקבִּילִית.

1. הגדרה של מקבילית.

אם נחתוך זוג ישרים מקבילים עם עוד זוג ישרים מקבילים, נקבל מרובע שצלעותיו הנגדיות מקבילות בזוגות.

במרובעים ABC ו-EFNM (איור 224) ВD || AC ו-AB || CD;
EF || MN ו-EM || FN.

מרובע שצלעותיו הנגדיות מקבילות בזוגות נקרא מקבילית.

2. מאפיינים של מקבילית.

מִשׁפָּט. האלכסון של מקבילית מחלק אותה לשני משולשים שווים.

תהיה מקבילית ABC (איור 225), שבה AB || CD ו-AC || ВD.

אתה צריך להוכיח שהאלכסון מחלק אותו לשני משולשים שווים.

הבה נצייר את CB אלכסוני במקבילית ABC. בואו נוכיח את זה /\ CAB= /\ СДВ.

הצלע NE משותפת למשולשים אלו; / ABC = / BCD, כזוויות צולבות פנימיות עם AB ו-CD מקבילים ו-CB חותכים; / DIA = / СВD, כמו גם זוויות צולבות פנימיות עם AC ו- ВD מקבילים ו- CB secant (§ 38).

מכאן /\ CAB = /\ СДВ.

באותו אופן, ניתן להוכיח שהאלכסון AD יחלק את המקבילית לשני משולשים שווים ACD ו-ABD.

השלכות. 1 . זוויות מנוגדות של מקבילית שוות זו לזו.

/ א = / ד, זה נובע מהשוויון של המשולשים CAB ו-CDB.
כְּמוֹ כֵן / C = / IN.

2. מול צדדים מקביליםשווים זה לזה.

AB = CD ו-AC = BD, שכן אלו צלעות של משולשים שווים ונמצאות מול זוויות שוות.

משפט 2. האלכסונים של מקבילית מחולקים לשניים בנקודת החיתוך שלהם.

תן BC ו-AD להיות האלכסונים של המקבילית ABC (איור 226). הבה נוכיח ש-AO = OD ו-CO = OB.

לשם כך, השווה זוג כלשהו של משולשים מנוגדים, למשל /\ AOB ו /\ בַּקָלָה.

במשולשים אלו AB = CD, כמו צלעות מנוגדות של מקבילית;
/ 1 = / 2, כזוויות פנימיות המונחות לרוחב עם AB ו-CD מקבילים ו-Secant AD;
/ 3 = / 4 מאותה סיבה, שכן AB || CD ו-CB הם הסקנטים שלהם (§ 38).

מכאן נובע /\ AOB = /\ בַּקָלָה. ובתוך משולשים שוויםצלעות שוות נמצאות מול זוויות שוות. לכן, AO = OD ו-CO = OB.

משפט 3. סכום הזוויות הסמוכות לצד אחד של מקבילית שווה ל 2 ד .

תוכיח את זה בעצמך.

3. סימנים של מקבילית.

מִשׁפָּט. אם הצלעות הנגדיות של מרובע שוות בזוגות, אז מרובע זה הוא מקבילית.

תן במרובע ABC (מצויר 227) AB = CD ו-AC = BD. הבה נוכיח שבתנאי זה AB || CD ו-AC || ВD, כלומר מרובע АВDC הוא מקבילית.
הבה נחבר עם קטע כמה שני קודקודים מנוגדים של מרובע זה, למשל C ו-B. המרובע ABCD מחולק לשני משולשים שווים: /\ CAB ו /\ СДВ. למעשה, יש להם אותו צד CB, AB = CD ו-AC = BD לפי המצב. לפיכך, שלוש צלעות של משולש אחד שוות בהתאמה לשלוש צלעות של משולש אחר, לפיכך /\ CAB = /\ СДВ.

במשולשים שווים, זוויות שוות נמצאות מול צלעות שוות, כך
/ 1 = / 2 ו / 3 = / 4.

זוויות 1 ו-2 הן זוויות פנימיות השוכנות לרוחב במפגש של ישרים AB ו-CD של הישר CB. לכן א.ב || CD.

באותו אופן, זוויות 3 ו-4 הן זוויות פנימיות השוכנות לרוחב בהצטלבות הקווים CA ו-BD של הקו CB, לכן, CA || ВD (§ 35).

לפיכך, הצלעות המנוגדות של המרובע ABCD מקבילות בזוגות, לכן זו מקבילה, וזה מה שצריך להוכיח.

משפט 2. אם שתי צלעות מנוגדות של מרובע שוות ומקבילות, הרי שהמרובע הוא מקבילית.

תן AB = CD במרובע ABCD ו-AB || CD. הבה נוכיח שבתנאים אלה המרובע ABC הוא מקבילית (איור 228).

הבה נחבר את הקודקודים C ו-B עם קטע CB. בשל ההקבלה של ישרים AB ו-CD, זוויות 1 ו-2, כזוויות פנימיות המונחות לרוחב, שוות (§ 38).
אז משולש CAB שווה למשולש CDB, מכיוון שיש להם צד משותף CB,
AB = CD לפי תנאי המשפט ו / 1 = / 2 לפי מוכח. השוויון של המשולשים הללו מרמז על השוויון של זוויות 3 ו-4, שכן הם נמצאים מול צלעות שוות במשולשים שווים.

אבל זוויות 3 ו-4 הן זוויות צולבות פנימיות שנוצרות על ידי חיתוך של ישרים AC ו-BD של ישר CB, לכן, AC || ВD (§ 35), כלומר מרובע
ABC היא מקבילית.

תרגילים.

1. הוכח שאם האלכסונים של מרובע בנקודת החיתוך ההדדית שלהם מחולקים לשניים, אז מרובע זה הוא מקבילית.

2. הוכח כי מרובע שסכומו פינות פנימיותצמוד לכל אחת משתי הצלעות הסמוכות שווה ל-2 ד, יש מקבילית.

3. בנה מקבילית באמצעות שתי צלעות והזווית ביניהן:

א) שימוש בהקבלה של צלעות מנוגדות של מקבילית;
ב) שימוש בשוויון הצלעות הנגדיות של מקבילית.

4. בנו מקבילית באמצעות שתי צלעות סמוכות ואלכסון.

5. בנו מקבילית באמצעות שני האלכסונים שלה והזווית שביניהם.

6. בנו מקבילית באמצעות הצלע שלה ושני אלכסונים.

מקבילית היא מרובע שצלעותיו הנגדיות מקבילות, כלומר. לשכב על קווים מקבילים

מאפיינים של מקבילית: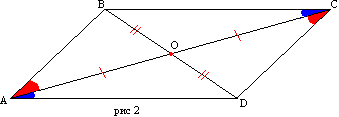
משפט 22. הצלעות הנגדיות של מקבילית שוות.
הוכחה. במקבילית ABCD אנו מציירים AC אלכסוני. המשולשים ACD ו-ACB חופפים, כבעלי צלע AC משותפת ושני זוגות של זוויות שוות. סמוך לו: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (כזוויות צולבות עם קווים מקבילים AD ו-BC). זה אומר ש-AB = CD ו-BC = AD, בתור הצלעות המתאימות של משולשים שווים וכו'. מהשוויון של המשולשים הללו עולה גם שהזוויות המתאימות של המשולשים שוות:
משפט 23. הזוויות ההפוכות של המקבילית שוות: ∠ A=∠ C ו∠ B=∠ D.
השוויון של הזוג הראשון מגיע מהשוויון של המשולשים ABD ו-CBD, והשני - ABC ו-ACD.
משפט 24. זוויות סמוכות של מקבילית, כלומר. זוויות הסמוכות לצד אחד מסתכמות ב-180 מעלות.
זה כך מכיוון שהם זוויות פנים חד-צדדיות.
משפט 25. האלכסונים של מקבילית חוצים זה את זה בנקודת החיתוך שלהם.
הוכחה. שקול משולשים BOC ו-AOD. לפי התכונה הראשונה AD=BC ∠ OAD=∠ OCB ו∠ ODA=∠ OBC שוכבים לרוחב עבור קווים מקבילים AD ו-BC. לכן, משולשים BOC ו- AOD שווים בזוויות הצלע ובזוויות הסמוכות. זה אומר BO=OD ו-AO=OS, כמו הצלעות המתאימות של משולשים שווים וכו'.

סימנים של מקבילית
משפט 26. אם הצלעות הנגדיות של מרובע שוות בזוגות, אז זו מקבילה.
הוכחה. תן למרובע ABCD צלעות AD ו-BC, AB ו-CD שוות בהתאמה (איור 2). נצייר את האלכסון AC. משולשים ABC ו-ACD שווים בשלוש צלעות. אז זוויות BAC ו-DCA שוות, ולכן, AB מקביל ל-CD. ההקבלה של הצלעות BC ו-AD נובעת משוויון הזוויות CAD ו-ACB.
משפט 27. אם זוויות הפוכותמרובעים שווים בזוגות, אז זה מקבילית.
תנו ∠ A=∠ C ו∠ B=∠ D. כי ∠ A+∠ B+∠ C+∠ D=360 o, ואז ∠ A+∠ B=180 o והצלעות AD ו-BC מקבילות (על בסיס הקביליות של ישרים). נוכיח גם את ההקבלה של הצלעות AB ו-CD ונסיק ש-ABCD היא מקבילית בהגדרה.
משפט 28. אם פינות סמוכות של מרובע, כלומר. הזוויות הסמוכות לצד אחד מסתכמות ב-180 מעלות, ואז זו מקבילה.
אם הזוויות החד-צדדיות הפנימיות מסתכמות ב-180 מעלות, אז הקווים הישרים מקבילים. אז AB מקביל ל-CD ו-BC מקביל ל-AD. מרובע מתגלה כמקביל בהגדרתו.
משפט 29. אם האלכסונים של מרובע חוצים זה את זה בנקודת החיתוך, הרי שהמרובע הוא מקבילית.
הוכחה. אם AO = OC, BO = OD, אז המשולשים AOD ו-BOC שווים, כיוון שיש להם זוויות שוות (אנכיות) בקודקוד O, כלואים בין זוגות של צלעות שוות. משוויון המשולשים אנו מסיקים שAD ו-BC שווים. גם הצלעות AB ו-CD שוות, והמרובע מתברר כמקביל לפי קריטריון 1.
משפט 30. אם למרובע יש זוג צלעות שוות ומקבילות, אז זו מקבילה.
תנו לצלעות AB ו-CD של מרובע ABCD להיות מקבילות ושוות. נצייר אלכסונים AC ו-BD. מההקבלה של קווים אלו נובע שהזוויות הצולבות ABO = CDO ו-BAO = OCD שוות. משולשי ABO ו-CDO שווים בזוויות הצלע ובזוויות הסמוכות. לכן AO=OS, VO=ОD, כלומר. האלכסונים מחולקים לשניים על ידי נקודת החיתוך והמרובע מתברר כמקביל לפי קריטריון 4.

בגיאומטריה נחשבים מקרים מיוחדים של מקביליות.

מקבילית היא מרובע שצלעותיו הנגדיות מקבילות, כלומר הן שוכנות על קווים מקבילים (איור 1).

משפט 1. על מאפייני הצלעות והזוויות של מקבילית.במקבילית, צלעות נגדיות שוות, זוויות נגדיות שוות, וסכום הזוויות הסמוכות לצלע אחת של המקבילית הוא 180°.

הוכחה. במקבילית זו ABCD אנו מציירים אלכסון AC ומקבלים שני משולשים ABC ו-ADC (איור 2).

משולשים אלו שווים, שכן ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (זוויות צולבות עבור קווים מקבילים), והצלע AC היא משותפת. מהשוויון Δ ABC = Δ ADC יוצא ש-AB = CD, BC = AD, ∠ B = ∠ D. סכום הזוויות הסמוכות לצלע אחת, למשל זוויות A ו-D, שווה ל-180° כחד-צדדית עבור קווים מקבילים. המשפט הוכח.

תגובה. שוויון הצלעות הנגדיות של מקבילית פירושו שקטעי המקבילים המנותקים על ידי מקבילים שווים.

מסקנה 1. אם שני קווים מקבילים, אז כל הנקודות על קו אחד נמצאות באותו מרחק מהקו השני.

הוכחה. אכן, תן || ב (איור 3).

הבה נצייר את הניצבים BA ו-CD לישר a משתי נקודות B ו-C של קו b. מאז AB || CD, אז האיור ABCD הוא מקבילית, ולכן AB = CD.

המרחק בין שני קווים מקבילים הוא המרחק מנקודה שרירותית באחד מהקווים לישר השני.

לפי מה שהוכח, הוא שווה לאורכו של האנך הנמשך מנקודה כלשהי של אחד מהקווים המקבילים לישר השני.

דוגמה 1.היקף המקבילית 122 ס"מ. אחת מצלעותיה גדולה מהשנייה ב-25 ס"מ. מצא את צלעות המקבילית.

פִּתָרוֹן. לפי משפט 1, הצלעות הנגדיות של מקבילית שוות. נסמן צד אחד של המקבילית ב-x והשני ב-y. לאחר מכן, לפי תנאי $$\left\(\begin(matrix) 2x + 2y = 122 \\x - y = 25 \end(matrix)\right.$$ פתרון המערכת הזו, נקבל x = 43, y = 18 לפיכך, צלעות המקבילה הן 18, 43, 18 ו-43 ס"מ.

דוגמה 2.

פִּתָרוֹן. תן לתמונה 4 לעמוד בתנאי הבעיה.

הבה נסמן את AB ב-x, ואת BC ב-y. לפי התנאי, היקף המקבילית הוא 10 ס"מ, כלומר 2(x + y) = 10, או x + y = 5. היקף המשולש ABD הוא 8 ס"מ. ומכיוון ש-AB + AD = x + y = 5 ואז BD = 8 - 5 = 3. אז BD = 3 ס"מ.

דוגמה 3.מצא את הזוויות של המקבילית, בידיעה שאחת מהן גדולה ב-50 מעלות מהשנייה.

פִּתָרוֹן. תן לתמונה 5 לעמוד בתנאי הבעיה.

הבה נסמן את מידת המעלות של זווית A על ידי x. אז מידת המעלות של זווית D היא x + 50°.

זוויות BAD ו-ADC הן זוויות פנימיות חד-צדדיות עם קווים מקבילים AB ו-DC וחתך AD. אז סכום הזוויות הנקובות הללו יהיה 180°, כלומר.
x + x + 50° = 180°, או x = 65°. לפיכך, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.

דוגמה 4.הצדדים של המקבילית הם 4.5 ד"מ ו-1.2 ד"מ. חוצה נמשכת מקודקוד זווית חדה. לאילו חלקים הוא מחלק את הצד הגדול יותר של המקבילית?

פִּתָרוֹן. תן לתמונה 6 לעמוד בתנאי הבעיה.

AE הוא חציו של זווית חדה של מקבילית. לכן, ∠ 1 = ∠ 2.

בעיה 1. אחת מהזוויות של המקבילית היא 65°. מצא את שאר הזוויות של המקבילית.

∠C =∠A = 65° כזוויות הפוכות של מקבילית.

∠A +∠B = 180° כזוויות הסמוכות לצד אחד של מקבילית.

∠B = 180° - ∠A = 180° - 65° = 115°.

∠D =∠B = 115° כזוויות הפוכות של מקבילית.

תשובה: ∠A =∠C = 65°; ∠B =∠D = 115°.

משימה 2.סכום שתי זוויות של מקבילית הוא 220°. מצא את הזוויות של המקבילית.

מכיוון שלמקבילית יש 2 זוויות חדות שוות ו-2 זוויות קהות שוות, ניתן לנו סכום של שתי זוויות קהות, כלומר. ∠B +∠D = 220°. ואז ∠B =∠D = 220° : 2 = 110°.

∠A + ∠B = 180° כזוויות הסמוכות לצד אחד של מקבילית, כך ש- ∠A = 180° - ∠B = 180° - 110° = 70°. ואז ∠C =∠A = 70°.

תשובה: ∠A =∠C = 70°; ∠B =∠D = 110°.

משימה 3.אחת מהזוויות של מקבילית גדולה פי 3 מהשנייה. מצא את הזוויות של המקבילית.

תן ∠A =x. ואז ∠B = 3x. בידיעה שסכום הזוויות של מקבילית הצמודה לאחת מצלעותיה הוא 180°, ניצור משוואה.

x = 180 : 4;

נקבל: ∠A = x = 45°, ו-∠B = 3x = 3 ∙ 45° = 135°.

זוויות הפוכות של מקבילית שוות, לכן,

∠A =∠C = 45°; ∠B =∠D = 135°.

תשובה: ∠A =∠C = 45°; ∠B =∠D = 135°.

משימה 4.הוכח שאם למרובע יש שתי צלעות מקבילות ושוות, אז המרובע הזה הוא מקבילית.

הוכחה.

נצייר את BD האלכסוני ונחשוב על Δ ADB ו- Δ CBD.

AD = BC לפי תנאי. הצד של BD נפוץ. ∠1 = ∠2 כפנימי צולב שוכב עם קווים מקבילים (לפי תנאי) AD ו-BC ו-BD חותך. לכן, Δ ADB = Δ CBD בשני הצדדים והזווית ביניהם (סימן ראשון לשוויון משולשים). במשולשים חופפים, הזוויות המתאימות שוות, כלומר ∠3 =∠4. וזוויות אלו הן זוויות פנימיות המונחות לרוחב עם קווים ישרים AB ו-CD וחותך BD. זה מרמז שהקווים AB ו-CD מקבילים. לפיכך, במרובע ABCD זה, הצלעות הנגדיות מקבילות בזוגות, ולכן, בהגדרה, ABCD היא מקבילית, וזה מה שהיה צריך להוכיח.

משימה 5.שני הצדדים של מקבילית נמצאים ביחס 2 : 5, וההיקף הוא 3.5 מ' מצא את הצדדים של המקבילית.

∙ (AB + AD).

נסמן חלק אחד ב-x. ואז AB = 2x, AD = 5x מטר. בידיעה שהיקף המקבילית הוא 3.5 מ', אנו יוצרים את המשוואה:

2 ∙ (2x + 5x) = 3.5;

2 ∙ 7x = 3.5;

x = 3.5 : 14;

חלק אחד הוא 0.25 מ'. אז AB = 2 ∙ 0.25 = 0.5 מ'; AD = 5 ∙ 0.25 = 1.25 מ'.

בְּדִיקָה.

היקף המקבילית P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1.75 = 3.5 (מ').

מכיוון שהצלעות הנגדיות של המקבילית שוות, אז CD = AB = 0.25 מ'; BC = AD = 1.25 מ'.

תשובה: CD = AB = 0.25 מ'; BC = AD = 1.25 מ'.

מקבילית היא מרובע שבו הצלעות הנגדיות מקבילות בזוגות.

למקבילית יש את כל התכונות של מרובעים, אבל בנוסף יש לה גם משלה תכונות ייחודיות. אם נכיר אותם, נוכל למצוא בקלות גם את הצדדים וגם את הזוויות של מקבילית.

מאפיינים של מקבילית

סכום הזוויות בכל מקבילית, כמו בכל מרובע, הוא 360°.
קווי האמצע של מקבילית והאלכסונים שלה מצטלבים בנקודה אחת ונחצו על ידה. נקודה זו נקראת בדרך כלל מרכז הסימטריה של המקבילית.
הצלעות הנגדיות של מקבילית שוות תמיד.
כמו כן, לדמות זו יש תמיד זוויות הפוכות שוות.
סכום הזוויות הסמוכות לכל אחת מהצלעות של מקבילית הוא תמיד 180°.
סכום ריבועי האלכסונים של מקבילית שווה לכפול מסכום הריבועים של שתי הצלעות הסמוכות לה. זה בא לידי ביטוי בנוסחה:
- d 1 2 + d 2 2 = 2 (a 2 + b 2), כאשר d 1 ו-d 2 הם אלכסונים, a ו-b הם צלעות סמוכות.
הקוסינוס של זווית קהה תמיד קטן מאפס.

כיצד למצוא את הזוויות של מקבילית נתונה באמצעות תכונות אלו בפועל? ואיזה נוסחאות נוספות יכולות לעזור לנו בכך? בואו נסתכל על משימות ספציפיות הדורשות: למצוא את הזוויות של מקבילית.

מציאת הזוויות של מקבילית

מקרה 1. המידה של זווית קהה ידועה, עלינו למצוא זווית חדה.

דוגמה: במקבילית ABCD, זווית A היא 120°. מצא את המידה של הזוויות הנותרות.

פִּתָרוֹן: בעזרת תכונה מס' 5 נוכל למצוא את מידת הזווית B הסמוכה לזווית שניתנה במשימה. זה יהיה שווה ל:

180°-120°= 60°

וכעת, באמצעות תכונה מס' 4, אנו קובעים ששתי הזוויות הנותרות C ו-D מנוגדות לזוויות שכבר מצאנו. זווית C הפוכה לזווית A, זווית D הפוכה לזווית B. לכן, הם שווים בזוגות.